Bureau, THE metric bureau

Posted on by wanderer

The humble metric system, as we have seen, was not established immediately. The legacy of the metric that I want to focus on is how it came to be, and what bureau was created to establish, motitor, standarize and update the metric.

The metric gathered support little by little from 1795, until, by 1875, the infamous Metre Convention, with the US being one of its founders! made it the International standard we all know and love, well at least one of these two is true.

The convention did not just stop at pushing for an international, standarised, metric system, no, they created one of the first bureaus. That we will be evaluating for now.

The 1875 one is the Weights and Measures: the International Bureau of Weights and Measures, or in its original french Bureau . They also established a conference (General Conference on Weights and Measures) and a committee (International Committee for Weights and Measures). Again, more on bureaus later, and committees, and conferences, and…

But why, by 1875, was it needed for a French mostassaf to be in charge of an international bureau at all? This is the interesting question. What is relevant for the metric system is not the use of units for measurement set by a national administration, but the fact that it implanted the idea that we all must use it and be raised in it.

The french Weights and Measures mostassaf did not came out of nowhere. Going back to the scientific homogenisation, we need to add the germans to the mix.

By 1841, 28 measurements of the magnetic field of the Earth where taken over a six year period. These measurements, all over the planet, where centralised by the “Magnetic Society”, or  Magnetische Verein in the original german. This was a society not a bureau, yet. As a society, the compromise was just to gather, standarise and share the measurements, so they could be useful across the planet. There was an extra benefit for endeabour, navigation. Like with the making of accurate clocks to measure longitude, an accurate description of the magnetic field allowed better seafaring transits, as the north and south magnetic poles of the Earth do not coincide with the geographical poles of the planet. Actually, the magnetic ones have a tendency to wander, quite fast indeed (hundreds of kilometres per decade), and even flip! (north becoming south). This was know for decades, or centuries, but was Gauss who in the 1830s started measuring its strength, and latter instigated the creation of the society, with international aims and ambitions.

Later on, the also german based Mitteleuropäische Gradmessung (Central European Arc Measuremen), linked with the need to measure the meridian to estimate the circunference of the Earth, and hence, the metre, was created on 1862. Interestingly, the Mitteleuropäische Gradmessung still exists in the form of the International Association of Geodesy, again, an association and not a bureau. By 1859 it was known that several meridians had not the same length, and that as measurement techniques would advance, the nominal definition of the metre would constantly change, even if so slightly.

A Catalan office —well aware of the Barcelona lie— Calos Ibañez e Ibañez de Ebro, was in charge of the International Association of Geodesy when in 1875 the Meter Convention was stablished. At the time of Carlos running these two pioneering international organisms, these were planned as contributing to increase precision in navigation, cartography and geography, as well as the emerging railways and telegraphs. Railways and telegraphs will come hunting us, but that’s for later.

So, despite the logic of unification being a concept from the particular French Revolution — which linked the metric with revolutionary ideas to make their political movement of decapitating kings (and many others) universal — the universalisation cached up four generations later, and, for the first time the particular Catalan mostassaf was not to be for a town, or state, but for all the planet!

From this story what I want to emphasise is that the importance is the base of knowledge of the standard, more than the standard itself, whatever it is.

How a continuously fighting world of nations came to decide that they could trust a base of knowledge? Moreover, how for the first time —unlike with mathematical, temporal, musical, and punctuational spontaneous standardisation — these nations decided to bureaucratise the process of standardisation with scientific geeks at the front of the first modern international institutions. This how process boils down to write laws that would be shared across borders and mutually understood, plus trust that the mostassaf would be available and willing to keep, share and not abuse its privative and privileged knowledge. Again, remember that the term mostassaf comes from an Arab religious figure of moral and measurement accountability.

So what makes the metric stand? Truly, a handful of things:
i) It was the first one designed from the get-go to be universal;
ii) it was based on natural units accessible, in principle, to anyone who had the time to finance the measure;
iii) it was easy to learn, aligning with mathematical notation, already quite universal and on base 10;
iv) it was set to work with technical and scientific communities;
v) the scientific communities were expanding, encompassing industrial and geodesical needs for better instruments, better measurements, faster and easier comparisons and sharing of technical information and better land and sea surveys for better administrative oversight (more on administrations later);
vi) its creators also kinda pushed for it to be adopted universally, following the spirit of revolution;
vii) there were not many alternatives at the time, to be honest.

Let us look at the last option (vii), alternatives? The only real contender for standard measurement used for scientific and technical applications by the end of the XIXc was the British Imperial system (still slightly kept by the US and Liberia). The imperial traces its roots to the standardisation of English measures, as designed by the 13th-century Magna Carta, but standardised by 1496, rectified in 1588 and made the British Imperial system by 1826.

We have the imperial length units. Let us look at these!. The basis is the foot, abbreviated as ft. The multiples are a yard as 3 ft, chain 3×22 ft, furlong 3×220 ft, mile 3×1760 ft, league 3x3x1760 ft. Well, it seems they were trying a base 3, but kinda gave up on it, soon. For the sub-units: twip 1/3^3×640 ft, thou 1/3×4000, barleycorn 1/3^2×4, inch 1/3×4, hand 1/3. OK, OK, kinda keeping with the basis 3 there, sometimes 4 as well, maybe inspired by the 60 for time — 3x4x5 — but also not quite. Now let us look at the distance units at sea: we have the fathom 6.0761 ft, cable 607.61 and nautical mile 6076.1… Now there is a base ten! But not much sense otherwise.

But a visual is better than thousands of words, and words of measures. Here is a side-by-side comparison of units of length in the traditional English system vs the metric one.

Comparison of English customary english and their interrelation with metric

For mass, the basic unit is the pound. Fair enough. But the shorthand for pound is lb. Yeah, we have seen that pound and livre are, in theory, referring to the same old Roman unit, but still, lb looks quite different than p or pn. Anyway, let us see its divisions: grain is 1/7000 lb, drachm is 1/256 lb, stone is 14 lb, quarter 28 lb, hundredweight 112 lb and ton 2240 lb. Little sense, but in base 12 or 60, like time, still makes no sense. For multiples it has base 14 (1, 2, 4, 800). Yet for divisions it has a basis, ehem, no consistent basis. A grain is 1/(14×500) — why 500? Well, a drachm is 1/2^8…

Sorry, I tried.

I will not even try the volume units. A beer pint is just a large half-litre drink.
Cheers to that!

The other option could have been the Burmese system. Myanmar still has traditional Burmese units of measurement. The Burmese system maybe has been maintained, in part, because for mass and volume it follows a neat base-two system, in which each unit is a factor 2 bigger than the previous — the metric being a factor 10 between units. Unfortunately, this is not the case for length and area; no, for length the Burmese system is a mess. For example, as of 2010, the state used miles to describe the length of roads, square feet for the size of houses, square kilometres for land area in cities, acres for agricultural areas, kilometres for the dimensions of the country. Still, when I was travelling there in 2015 I did check if they were the US of Asia for the metric, but for reasonable driving they did use km for distances to places and km/h as road speed limit indicators.

So, form the above list, let us focus on points (iv) to (vi): the need, willingness and expansion of technical and scientific domains beyond national borders (more on nations later).

The expansion of the metric is interlinked with these technical and national advancements and ended with some of the first bureaus on the planet.

The republican French, to celebrate the 10th anniversary of the Revolution, did a technical and industrial fair in 1798. This was not much international, as they were in the middle of intense wars, still not called Napoleonic. At the exposition they showed devices demonstrating the new metric system of metres, grams and litres, and, following European fair traditions, they had prizes for outstanding products, mostly fabrics and textiles, but now including innovative technical and industrial devices. One of them was the precursor of the modern pencil, and pencil colours.

They held three more expositions until 1806, and then new ones shall happen every 3 years; this allowed for enough new inventions, geographical explorations, arts, sciences and devices to be developed between events. But by 1809 France was indeed in the middle of the Napoleonic wars.

By 1819 the now French kingdom restarted the expositions, which happened roughly every 4 years.

Then the Kingdom of France decided to revolutionise a bit again and become the kingdom “of the French”. Notice the difference; it will be important later on. Then they decided to make an exposition every 5 years, starting in 1834.

The 1844 one was quite a success internationally, spawning similar fairs in other nations — Bern (1845), Madrid (1845), Saint Petersburg (1848), Lisbon (1849). Then in 1849 there would be the last national exhibition, as in 1851 the British did their Great Crystal Palace Exhibition, which for the first time had the dimension of a world, and not national, fair. From there on, world exhibitions would happen regularly, a bit like the Olympic Games now, and cities would compete with each other to host the event.

These World Fairs, or “the Expos” for us old enough to remember them being a thing, initially were great opportunities for showcasing the most advanced scientific and technological discoveries of the time. This was especially important in an era when more efficient and powerful steam engines, steel, locomotives, rails, and later electricity and telegraph were taking over the European nations and their colonies. In these events, industrialists and scientists from around the world could meet and agree on stuff.

That stuff, my friends, was the metric system, which by the end of the Napoleonic Empire, like decimal time, had gone down the drain. Napoleon reintroduced the customary units, but retained the metre and kilogram for these units to be compared against. The metric systen was also taught at schools and academia. It was simple to teach, as we have seen.

Meanwhile, the metre lived on in other states that were under the influence of the French Empire and retained the metric system, like the Netherlands, Switzerland, and Piedmont, later the Italian kingdom.

And the US, of all places, had a central role for the metre. The Coastal Survey Office, since its inception in 1807, but really by 1836, standardised all the coastal measurements with the metre as its basis.

And even nations that escaped Napoleon, like Portugal, by 1814 adopted the metre, though retaining the traditional names when needed.

Spain, as we have seen with the Catalan measures, had a diverse set of systems. But by 1849 decided to standardise measurements with the metre and kilogram, and by 1851 decided to conduct a survey of the state. The Spanish bureau of measures also adopted and developed new measurement tools to compensate for thermal expansion of the standard metre rods. That made the use of the metre more precise and more manageable. Then it provided standard metres to the Egyptians, and the standard was used throughout France and the German Confederation.

On the first French Universal Exposition in 1855, the Swiss had finished, and presented, their official map with the metre adopted as unit of length, and this was awarded a medal.

Moreover, the Congress of Statistics was held in Paris at the same time as the exposition. There, statisticians, probably tired of wasting time making conversions of units, and probably not happy with the metre being kept by a France-based mostassaf, decided to settle on a uniform decimal system of measures, weights and currencies.

Again, the US pushed for the metric system by 1866. One of the bases of precision balances was in grams and kilograms. In 1866 (made in Bangor, Maine, where I’m writing this now) the legislative organ passed the Metric Act, which defined the metric system in terms of customary units rather than with reference to the international prototype. Interestingly, this anchored the customary measurement units to that of the metre, even if it legislated the other way around.

Then, at the 1867 Exposition Universelle, again in Paris, the statistician geeks formalised the universalisation desire with the creation of a Committee for Weights and Measures and Monies. Now it would not be the French revolutionaries calling for universalisation, but a bunch of geeks with the ears of wealthy industrialists interested in easier technical standards.

That committee finally, after the Franco-Prussian War, created the Bureau, the International Bureau of Weights and Measures, with two governing organs and the headquarters. The newly created German and Italian states already adopted the metric system as their standard. These nations now were part of the bureau, which was tasked to facilitate the standardisation of weights and measures around the world. The bureau had three parts: a conference as a forum for representatives of member states; a committee of metrologists as an advisory board of high standing; the headquarters as the meeting place and laboratory facilities that inform the decision and advisory bodies for decision-making. Corporations, interestingly, often work similarly to that: the conference would be the shareholders’ meeting, and the committee the board of directors.

The Catalan Carlos Ibáñez e Ibáñez de Ibero — the head of the Spanish survey and national measures institute, and maybe familiar with the mostassaf concept — was one of the main pushers of an international standard based on the metre. By the bureau’s creation, he was made the initial president of the committee, the Permanent Committee of the International Metre Commission (confusingly, also named International Committee for Weights and Measures and General Conference on Weights and Measures; do not ask). Being Catalan of origin, Ibáñez, since 1853, also impulsed the remeasurement of the “Barcelona lie”, that is, the Paris meridian, extending the measurement from the Shetland to the Sahara. That effort, and other European meridian measurements, awarded him the first presidency of the International Geodetic Association by 1867.

The 1875 Metre Convention put the decision-making of the standard measurement of the planet in a bunch of nation states’ hands. The original signatories being Argentina, Austria-Hungary, Belgium, Brazil, Denmark, France, Germany, Italy, Peru, Portugal, Russia, Spain, Sweden, Switzerland, Ottoman Empire, United States of America (yeah, you have seen it well, US is here!), and Venezuela (which no longer ratifies the Metre Convention).

Metre Convention on the planet. Dark green, member states; light green, associate states; red, former member states; light red, former associate states.

Interestingly enough, the metre is also not completely dominant in the UK, where the standards for the metric system, and the metal piece that defined the kilogram for 160 years, were made.

In the US there is also the fun fact that, unlike the UK, industry is not forced to use the metric system for all their products, despite being one of the original seventeen signatory nations to the Metre Convention.

Therefore, when NASA asked its suppliers to work with the metric system, but one of its suppliers, who procured thrusters for a probe to Mars, worked with customary units of pound-force-seconds, the result of such an integration of two different systems was that the poor Mars Climate Orbiter probe simply went on its sweet way to Mars just to descend to about 57 kilometres above Mars’ surface, instead of its planned orbit at about 150 kilometres. At that height, and without enough angular velocity, and with the drag of the tenuous Martian atmosphere, the orbiter simply produced a nice flame in the atmosphere.

That is the price of not having a unified unit system.

So being the first, and not having many alternatives, plus being relatively memorable and accessible (had to knock at the Parisian mostassaf from time to time, but was a cool person), made the whole system go global, or pay the price if not.

The metric system simply illustrates how national administrations and gatherings of world representatives agree to standards. In the metric case this quasi-standard emerged through technological need, the ease of communication that allowed repeated forums where actors interested in standardisation and sharing could gather and lobby in a uniform way, the relative ease of the new system and its spirit of universalisation, and a specific individual with the right connections and maybe aware of the connection between moral and measurement accountability through an old mostassaf legacy in our lands.

If we compare the metric to the other standards that we have seen — mathematical and musical notation, francas, timekeeping and punctuation — all of these share similarities. Technical advancements for clocks creation and the need of better measurements for navigation and trains in the case of timekeeping; more communication, new instruments and bigger orchestras for music; economic interest for francas; facilitation and economic dissemination for punctuation. With the exception of the calendar, none of these standards had behind them the will of the states or nations. And even the legislation for calendars happened at a customary and slow attrition, state by state, without an international gathering, convention or bureau leading it.

Like the weights and shekel 3000 years ago, we can look at more modern cases of this seemingly spontaneous standardisation originating by the end of the 19th and beginning of the 20th. For example, if you ever used headphones, the connector, or “jack”, to the sound device might have always been the same diameter 1⁄4 in and shape, or have only two–three standards (1/8). Another piece quite familiar to most of us nowadays is the keyboard I am typing this on, which is an almost international standard, called QWERTY, named after the order of the letters on the first keys’ row. Looking elsewhere, the bicycle chain is 0.5 in between pins and 5⁄16 in for roller diameter. The size of cargo containers, 8 ft wide by 8 ft 6 in high and 20 or 40 ft long. Yeah, metric did not make it for jack, bikes and cargo, damn.

More on the emergence of these (and other) standards later.

What we can infer, however, is that standardisation follows a mixed route of informal conformity by useful means of exchange, plus a forcing pace by institutional action. Then, in an interconnected, and colonially dominated, world, the metric system in particular shows the first, or one of the first instances, of how slow attrition to shared standards could be hastened by gatherings and lobbying committees. And how that commitment results in autonomous bureaus that horn in their task. In the experience of THE Metric, the legislative power of national institutions could be weaponised to steer reluctant populations that were happy with their local traditions and units, however clumsy, to adopt new and bureaucratised standards countries away, instead of their local mostassaf. Or shield them, as in the US, however clumsy. A new state-sponsored universal education could get away with old traditions by educating children in new, maybe more memorable, systems.

With the dreaded metric we can see how all the pieces are falling into place to have the ruleset to ask our question: what does humanity want? But before that we need to go through the emerging bureaus and other international organisms that, for now, rule, the World.

Previous

THE Metric, system

THE Metric, system

Posted on by wanderer

And as with many things in these writings, it all starts with the French Republic, the first one, or the French Empire, the first one.

But before, we need to go back to the Babylonians, again.

There is evidence that as far as 3,000 years ago, Mesopotamian merchants established a standardised system of weights that later spread across Europe, effectively forming the first known common Afro-Eurasian market. In a study, thousands of objects used as standards of weight over the course of 2,000 years in an area from Ireland to Mesopotamia weighed nearly the same amount — between 8 and 10.5 grams.

This “spontaneous” standardisation, though, started by copying the Mesopotamian standard, called the shekel, which later became a coinage system, and now is the name for Israel’s currency.

In fact, coins are no more than a stamp into a piece of metal to say that such metal is the value that it claims to be, with the purity of the metal that the stamp issuer claims.

Basically, at some point many cultures in antiquity decided that if a certain king or organism put — insert here his or her face, or symbol, or god — onto a round and flat piece of metal, that would be enough for people to believe that such a metal piece was of such-and-such quality and mass. That is why “pound” is both a weight and a coin. It kinda worked because we still have these small pieces of metal going around in almost every place on the planet, with few counterfeit ones, and many, many faces of mostly old — often dead — dudes.

Therefore, the whole system is based on trust that all the coins are made according to the same mass and purity standard, and that such a standard is known by everybody who is using it. We will see more of the importance of trust in later chapters.

But trust is only needed for the value part of the standard. As we have seen with mathematical and musical notation, punctuation, and francas, a degree of intent and shared interest in communicating, — plus actual political and militaristic control of peoples, and some degree of prestige—, also does the trick, without much need of trust.

But for now, let us jump to the United States now that I am writing this here. Maybe people from the US, and the Myanmar government, do not especially embrace it, but children do not like the Babylonian time keeping much either. Children tend to prefer the legacy of the Republic, the French Republic, the first one.

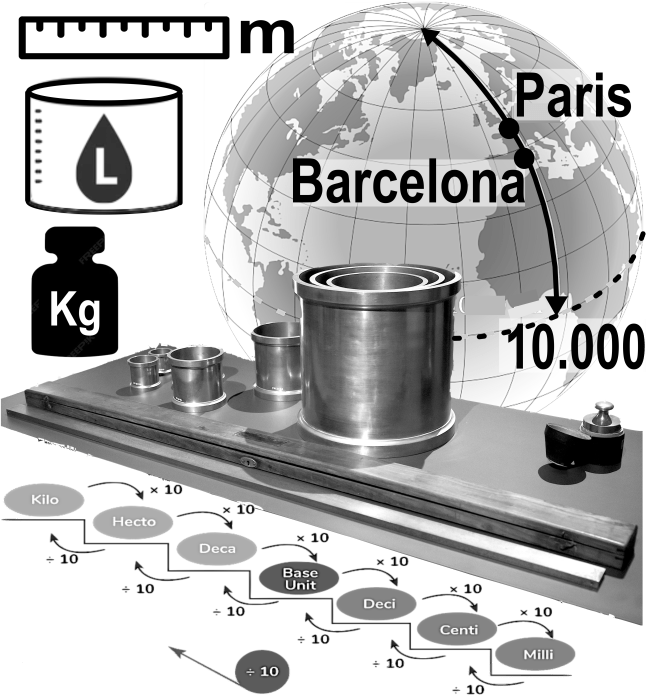
That is, the metric system. To clarify.

The metric, with a limited set of units that follow a decimal scale, and a conventional nomenclature linking base-10 “words” to multiples (from Greek) — deca, 10, hecto 100, kilo 1000… — and divisions (from Latin) — deci 0.1, centi 0.01, mili 0.001 … — rules the world: the world’s measures (not time; time still is Babylonian, as we have seen).

Compare the French metric to the Babylonian time, with base-60 seconds and minutes, but a 24-hour day, 7-day week, 28- to 31-day months, seasons starting on the 20th or 21st of some months, and years, with some being one day longer than others. Children love to learn the metric, not so much timekeeping.

Before we had a universal measurement system, each yardstick would have a local reference to which it would be computed. For example, going to a marketplace you pour your grain into a container that would tell you how much grain you had and you could sell. Of course that depended on the actual container, and it might change marketplace to marketplace. To this day, I still find some of these containers in market squares set in stone.

But these containers for goods such as grains and olives were not straightforward to describe. For example, for volumes in Catalan-speaking lands we had this:

The quartera was equivalent to the capacity of the container [this container being the one at the market-squares] of the same name. [...]. The aimina is a very old measure that appears in a large number of documents. As submultiples [of the aimaina] there were: the measura, the sester, the cossa, the punyera, the picotí, etc. The barcella was the measure used in the [balearic] islands (where it was divided into 6 almuds or 1/6 of a quartera) and in the Valencian Country (where it was divided into 4 almuds, or 16 quarterons, or 108 mesuretes, equivalent to 1/4 a taleca, or 1/12 of the cafís, or 1/2 fanecà [also the name of a area unit equivalent to 833.3m2, or the land surface that can be cultivated with one faneca of grain ]. The barcella was also used in Tortosa, where it was equal to 3 cutxols, or 6 almuds, or 1/25 of the cafís. For forment [wheat], barley, oats, etc., the cafís is just 25  barcelles [adjusted to the edge of the container]

Did you get dizzy with that trainload of measure names, specific for each township or territory AND to which kind of good it was being measured? I did, and is my language.

This system was so complex that a profession, the mostassaf (accountant), was needed to make sure the measures were respected. The mostassaf was a profession inherited from the Muslim muḥtasib, inspector of public places and behaviour in towns. Measurement was, indeed, in need of public behaviour. Muḥtasib comes from ḥisbah, or “accountability”. Interestingly, the term also has both meanings in English: moral accountability, and how to account for economic transactions (the profession being accountant). This connection between debt and morality is deeply explored in — slightly cherry-picked and immensely thought-provoking — David Graeber’s 5000 years of dept. In the Aragonese territories the mostassaf had to keep the original measurement patterns and check that the copies had enough precision with his personal seal for the canes (sticks, length), balances (balance, weights), and all the volume units that we have seen.

What is interesting for the linguistic part is that, although these measures varied from town to town, or mostassaf to mostassaf, they were called the same. So these ‘measures’ were similar enough from one place to the neighbour that everybody agreed for that to be the standard, but not quite. Again, like with languages, the measures might have drifted the further away you went from one place, while the name itself might be the same. As I often heard in India: same same, but different.

In fact, that same same but different, and terminological mess is one of the reasons why the estimation of the size of the Earth used by Columbus was so wrong.

Part of the computations were using the measurement that Eratosthenes of Alexandria did more than 2,000 years before. His measure was about 252,000 “stadia”. But if I tell you that your dog measures 0.008 stadia, you still would not be sure of how long your dog is. For that you would need to translate it to a measure that you are familiar with. Depending on what the equivalences are, your dog could measure 0.00012 km or 95 inches.

This was the problem faced by Columbus and many of his contemporaries. Nobody really cared to pay anybody to measure, on land, the distance between Alexandria and a place south of it where there was no shadow in a well on an equinox day, the Tropic of Cancer.

These armchair thinkers simply quoted Eratosthenes, and the people who copied him over the millennia. But the Olympic games were long gone, and not many “stadion” existed as a reference. Even today, when we can measure archaeological remains of stadia and historical sources, experts argue that the unit could be anywhere between 150 and 210 metres.

Ptolemy took the lower estimation of Earth’s circumference. Later the Arabs translated previous estimations of the circumference of the Earth by Posidonius, Strabo, Hipparchus, Aryabhata and Pliny. They themselves did some extra measurements lead by Al-Khwarizmi, Al-Biruni and Al-Farghani. All of these translations and new measurements, confusingly, was converted to ‘miles’.

However, naming something the same does not mean it is the same.

‘Miles’ for the Arabs are not the ‘imperial’ ones. Moreover, something that at this point should surprise no one: the mile the arabs where using to translate previous Earth size estimates, and their new measures, has no clear conversion to modern units. An Arab mile from these text being interpreted as anywhere between 1,800 and 2,000 metres. Not so bad but still a 10% margin.

In any case, the same number of miles will be about 1/3 bigger or smaller depending on which mile it is. Same same, but different indeed.

This convoluted process ended up being taken by some people, Columbus among them, to be 25–33% smaller than the modern estimate of about 40,000 km for Earth’s circumference. For convenience, to have funding from inland Castilian monarchs with little experience with seafaring, Columbus took the ‘short yardstick’. Lucky he, and the Castilians, was that there was a continent on the way, just shy of 30% of the total landmass of the planet. Not a small serendipitous crash.

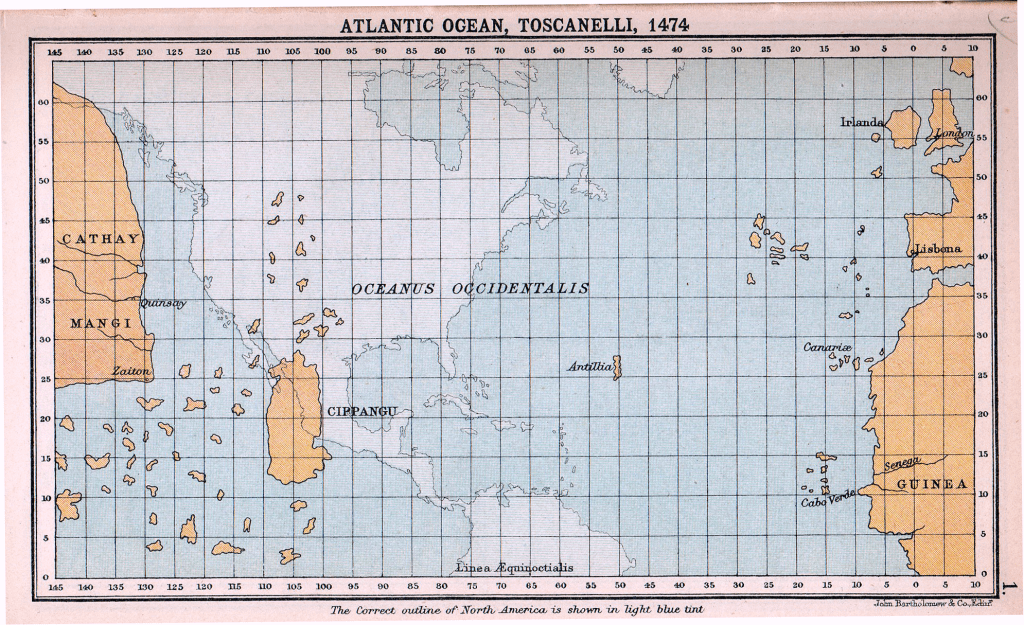
Interpretation of Toscanelli vision of the Atlantic, with approximate placement of the far east (Japan as Ciappangu) and the mythological Antilla island.

This naming confusion, together with other miscalculations like the size of the Eurasian continent, the distance to Japan from the mainland, and the existence of a mythological ‘Antilla’ island east of Japan, made Columbus pitch that he will reach some land about 4,400 km west of the Canary Islands.

He was off by almost 16,000 km if his aim was to reach the vicinity of Japan!

The Taxing Metric

With a continental miscalculation one can see how having universal measurement units helps — unless one has profound ignorance of the continents that exist on the planet to save the day, but condemn, decimate, mutilate and abuse millions of humans who will fall under the administration of that deceiving money-graving person (for more on Columbus’ administration in what was called the ‘Antilles’, modern-day Hispaniola and Cuba, read the reports from his contemporaries).

As transcendental — or not — history-changing Columbus’ blunder and continental serendipity is, this is not the reason for the metric system.

The infamous metric, sadly, comes mainly for taxes, French taxes to be exact.

The metric’s inception was an attempt of unification of measures within France. The kingdom was born out of annexing neighbouring administrations over the centuries, but keeping the local structures mostly intact. Therefore, by the late 18th century it had many different regional measurement systems. The monarchy under King Louis XVI, well on its way to absolutism and centralism, ordered the Academy of Sciences to come up with a unified system. That process was still going on when the Revolution unfolded.

Nowadays, France seems like quite a homogeneous part of the world. Obviously ALL French people wear black-and-white horizontal striped shirts, red-capped berets, are thin and tall, with slim black trousers, both sexes have a spiralling moustache that they continuously apply wax to, making it pointy, while holding a baguette under their arm. While walking, they drink coffee from a delicate porcelain coffee mug sustained only with two fingers.

Beyond exaggerated stereotypes, such clichés just show that such reality is impossible, even more in the case of France.

Even today France is one of the most diverse countries in Europe. Up to nine languages are natively spoken there, and its modern borders were not established until after WWII. Moreover, not even kisses are standardised! Depending on which part of the country you are in, you give two, three, or up to four cheek kisses to greet each other. Or you start from the left or right, and these do not even properly overlap (see map).


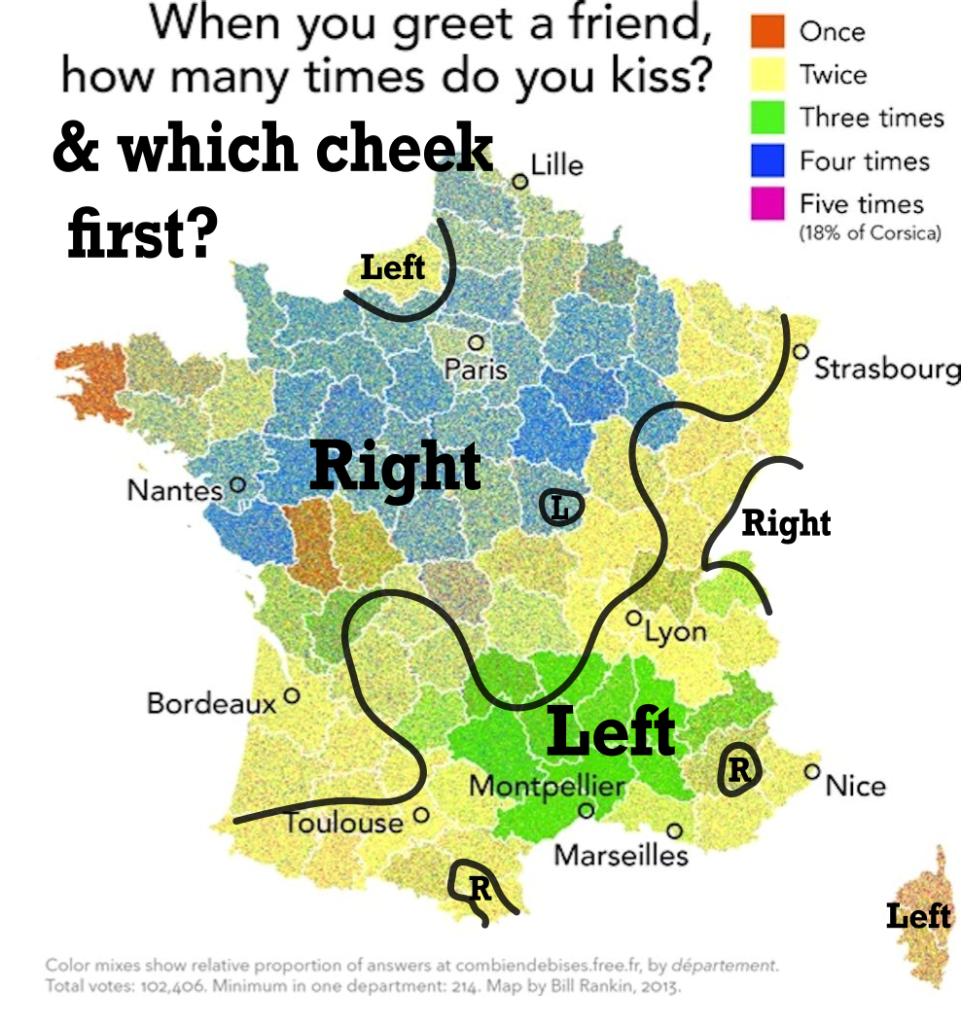
Adapted from Bill Rankin and Armand Colling (parlez-vous le français?, cheek main direction).

The apparent homogenisation of the metric system actually comes out of that diversity. Citing directly from Wikipedia here:
“on the eve of the Revolution in 1789, the eight hundred or so units of measure in use in France had up to a quarter of a million different definitions because the quantity associated with each unit could differ from town to town, and even from trade to trade […] These variations were promoted by local vested interests, but hindered trade and taxation [20][21].

Notice the taxes there. Paris’ post-1789 administration, but pre-republican, had an evident difficulty to grab taxes. The royal piecemeal system evolved over the centuries as a complex administrative, legislative, and executive mosaic landscape that emerged after the ending of the Western Roman Empire, with the monarch only having token powers in much of the lands it had nominal sovereignty over.

The Sun Kings grabbed more and more power over the 17th and 18th centuries, and, simultaneously, squeezed more the French finances. Finally, in a time pre-revolution when finances were in deep trouble — see the origins of the French Revolution — the need emerged to centralise local measures and make them uniform across the land. That kingdom-wide standardisation would nominally aid commerce and taxation.

This standardisation started with length. Scientists already wanted to standardise units — we love that; the fun is in figuring things out, not wasting time in conversions. An initial attempt was metro cattolico, from Greek metron (measure), which is the same root as the metric in music: the counting or rhythm of the melody. It also accounts for meteorology, which is the study of the weather, or accounting for weather conditions one particular place experiences — so much rain, so much cold/hot, so much wind, etc. Accountability can be moral or economic, but, it seems, can also be climatic And in some languages, like Spanish, the weather is called el tiempo, or the passing of time, linking change/weather with meteorology again: a tempo. And cattolico is the same sense as the Catholic Church, which simply means universal church, in opposition to others that were not as universal as them. This did not last long, though.

Anyway, the Royal (at that point) académie des sciences decided to base the whole standardisation of measures on the metre. It being a 10,000,000 division of the distance from the North Pole to the Equator following the line that passes through the Paris Observatory, not far from Notre-Dame cathedral. This distance is the Paris meridian arc, at 2°20′14.03″ East. Since this is only ¼ of the circumference of the Earth, the planet has a perimeter of roughly 40,000 km (easy to remember), depending on where you measure it, as it is not a perfectly spherical object but an oblate spheroid.

Moreover, conveniently, the current metre is about two cubits — which is based on human arm length from the tip of the fingers to the elbow — a step (the distance of a human — you know — step), and a yard (the tip of the fingers to the opposite soulder). These length units were widespread in pre-French-Revolutionary Europe, the Mediterranean, and Western Asia.

However, it would not be until 1799 when the current metre was established, and it involves Barcelona, and a lie. Choosing the meridian that crosses the Paris Observatory as the basis of 10,000 km is not only useful for nationalistic reasons. The meridian also allows a long section of land, from sea to sea, in a North–South line in Europe, where distances can be measured with precision, with latitude at each end point, by sea level. The seaside north of Paris is Dunkirk, and to the south the more famous Barcelona. The distance between the two is about 1,075 km, measured by November 1798. The survey manager to the south made an error, estimating the latitude of Barcelona wrong. He remeasured it, but kept it secret. This error would not be disclosed until 1836.

Then académie des sciences used the basis of the metre and water to set the other two standards: weight and volume. The unit of volume shall be that of a cube whose dimensions were a decimal fraction of the unit of length, a.k.a. cubic decimetre, or litre. Then, the weight of distilled water at 0º Celsius (the temperature of melting ice — do not get me started on temperature scales, now that I’m in the US) in that cube shall be, wait for it,

the grave.
(from Latin gravitas, i.e. weight)
This was accepted on 30 March 1791.

They did not like the grave, or the little grave, which they called gravet (one thousandth of a grave). It did not follow the neat deci, centi, mili categorisation — it should have been milligrave. Then, by 1795, already a republic, the national assembly changed the metric unit of weight to gram, from the Byzantine Empire: one twenty-fourth part of an ounce (two oboli) corresponding to about 1.14 modern grams. So kinda convenient, also a similar name to grain (like wheat grain), though 1 gram is about 20 grains.

Then our beloved litre, defined in 1795 as the volume of one cubic decimetre of water at the temperature of melting ice (0 °C). However, since the kilogram was redefined to be the mass of 1 cubic decimetre of water at its densest point at atmospheric pressure (about 4ºC), then the litre and kilogram no longer match. The story is more complex, but we will leave that for the fearful bureaus — coming soon. The word litre comes from the same root as livre (pound), a unit of weight and the name of the French currency until that moment. Again linguistics shows the equivalencies on peoples minds of volume and weight, which make no actual sense, but we are shaped that way.

For much talk of the litre, it is no longer a unit of the International System, but more on that later. It is still indeed part of the metric system, for the division in multiples of ten, and the kilo, deca, deci and other names for the multiples of 10.

In 1795 the republican France was eager to get more standardisation down their belts. Beyond the m, l, kg trio, they got to standardise the are (100 m2) for area, the franc for currency (from France) —s a side note, the currency was the third one to be on base 10, after the US currency and the Russian one — and the stère (1 m3) of firewood (from Greek, stereós, solid, that’s why people take steroids to have solid muscles, not sure if that’s true but I’ll not bother to check). Yeah, firewood needed standardisation. We are asking what does humanity want; apparently back in 1795 they wanted firewood to have a primary unit of standardisation. The world sure changes.

The académie des sciences and the national assembly tried to standardise time too. It would have been decimal: one republican second being 1/100,000 of a day, so bout 0.864 of a Babylonian one, which actually is closer to one human heart beat per republican second, as the heart usually beats a bit faster than once per babylonian second. But we have seen how that went down the drain because the British did better clocks, as we have seen. So much for French vs British clichés and stereotypes.

Beyond seconds’ failure, the metre and weight also failed at the end of the French Empire, the first one. Well, their definitions, to be exact. Because exactitude was the problem.

For the metre, the “Barcelona lie” had been intended to ensure international reproducibility. Who would have thought! This was impractical. So the world lost tourists from all nations coming to Barcelona to measure its latitude and distance to Dunkirk. The city has other issues with tourists, though. Beyond that, the “Barcelona lie” was a small error compared to the “gravitational lie”, i.e. the Earth’s surface has no exact gravity everywhere on its surface, making the planet not a spheroid but a geoid: a kind of potato, a really smooth potato. In actual terms that means that the meridian arc that crosses Paris’ Observatory is about 2 km longer than estimated, so 10.002 kilometres. Or the metre being 0.2 mm shorter than it should be.

In any case, the meridian measure was abandoned and a metal bar held in Paris was the actual definition. We now had a 19th-century French mostassaf. Not a great progress, but at least the units were easy to remember.

For the gram, the “be water, my friend” did not work either.

Humans tend to put our mind into precision once we get a target. The target was universalisation that could be measured. A mass standard made of water was inconvenient and unstable. It depended on the pressure, which was dependent on other measures. Moreover, even pure water is not “pure water” everywhere in the world. Making it “pure” might be difficult if one only wants H2O molecules in it. And beyond being H2O, the ratio of oxygen and hydrogen isotopes (different masses of an atom) is not constant: it might “weigh” differently even though it occupies the same volume.

Therefore, since you already went to the French mostassaf to ask for a copy of a metal bar for the metre, since you were at the door, why not ask for a copy of a kilogram too? Thus, they made a provisional mass standard of the grave, ehem, kilogram.

This was THE metric for much of the beginning of its history, that is, until the fearful bureaus arrived!

Previous

Oh!, punctuation

Next

Bureau, THE metric bureau

Mathematics, universal not the way you think

Posted on by wanderer

Before moving to the quasi-universal metric system —which includes the archaic Babylonian timekeeping— let us focus on probably the first universal lingua franca: mathematics. And not mathematics as in “the language of the Universe”, but mathematics as in “the set of codes, rules, concepts, and ideas that are shared and approximately mutually understood by any human using them”.

As we will see, many linguas francas originate as an often simple code (compared to a general-use language), developed rather quickly to serve a specific function. In many cases, that function has been simple commerce and exchange, where the number of items to “exchange” is limited, and the rules of the game are simple —possibly including locally standardised accounting, such as produce and monetary units, and standardised measures like weights, surfaces, and volumes.

The linguistic and symbolic part of mathematics, therefore, is not so different from commercial linguas francas. What sets it apart is that, as of the 21st century, virtually everybody using “mathematics” as a functional system —mostly algebra and calculus— uses the same notation. In other words, it is universal.

This is not surprising: when one thinks about a universal language, one often refers to mathematics. However, like with timekeeping, how we came to the specific and well-known set of symbols +, =, ÷, ∞, … has its own history.

Mathematics and mathematical notation, although common in the current world, took centuries to take shape. Over generations, it was agreed upon by scientific, technical, and mathematical communities in Europe, the Middle East, and South Asia to use the same kinds of symbols, numbers, and conventions to refer to the same concepts.

Interestingly, these “concepts” themselves were (and are) thought to be universal, even beyond the human realm —i.e. the number 3 is the same in all parts of the Universe. Therefore, unlike goods and commercial language, which had local characteristics, mathematical notation is expected to be written in the same way by everyone using those concepts and wanting to share them, regardless of location. The same applies to signs and symbols like +, =, ÷, ∞, which any reader would most likely recognise regardless of the language being used.

For some reason, written mathematics —often calculus— has always been something of a special case in many cultures. We can write numbers as they are spoken in a given language —like zero, one, two, three in English, or cero, un, dos, tres in Catalan. But often, across many writing systems, numbers have been chosen to be represented by symbols, for example: I, II, III… (Roman, no zero), 0, 1, 2, 3… (Arabic, from South Asia), 𝋠, ·, ··, ··· (Mayan, perhaps the 0 doesn’t display in Unicode), 零, 一, 二, 三 (Chinese, 零 meaning something less than one, yet not nil).

These examples show that from early on, people decided it was better to simplify numerical notation —to the point that doing otherwise seems like suffering. Try writing down the year the Portuguese took control of Malacca in the Common Era calendar: one thousand five hundred and eleven, or one-five-one-one, if simpler. Write it. Stop reading.

How do you feel?

I bet it’s a pain, and it feels right to simply write 1511. A similar thing applies to phone numbers. If you’ve ever used certain online platforms that do not allow phone numbers to be exchanged, you cannot send them using digits. A workaround is to write them out in words —for example, “one hundred and twelve” or “eleven two” instead of 112. It’s not much more effort to spell the numbers, but it still feels like a pain knowing that a shorter, cleaner alternative exists.

Although people must learn two different systems to write numbers —instead of just the phonetic one— which might seem like more effort, in the long run, simplification tends to dominate. This preference for simplicity is similar to what we will see in francas, linguas francas: the adoption of a shared, simplified, functional language is preferred over a fully developed one. So, the basis of our mathematical universality might have less to do with the Universe and more to do with a universal feeling: tediousness.

In the case of mathematics, despite numerals having been used symbolically for millennia, the simplification of other concepts —like “sum”— into symbolic script is a relatively recent development. This is exemplified by the fact that signs equivalent to + are not found in many older written systems while there is a diverse set of equivalent signs to 1. Things like +, and -, are known as “operators” in mathematical terminology. Interestingly, many of these operation symbols —unlike some numerals that are simply dots or lines —have phonetic origins. Phonetic symbols were already present in some numerical systems, like one of the two Greek numerical systems, where they would use Π as five (short for pente, 5 —Π being pi, capital P in Greek), or Δ as ten (short for deka, 10 —Δ being delta, capital D). The other Greek numerical system simply assigned the order of the alphabet to the numbers, \alpha being 1, \beta being 2, etc. Many societies around the globe have developed advanced mathematical notations. However, none of them used algebraic notation like + to mean “sum”. Other mathematical systems worked with geometry to describe concepts, or used written linguistic statements.

Linguistic statements was the European method too. Before symbolic expressions, European mathematicians wrote their sums. For example, they would put on paper: “3 plus 5 equals 8”. Since that was a pain —like writing numbers in words— they simplified it to “3 p 5 e 8”. The operations had no proper symbols, just words or shortened initials understood by context. In fact, the sum symbol, +, is one of the earliest to appear in written arithmetic. Although it originated by mid-14th century, it was only commonly used by the 15th century. While there’s no universal agreement on its origin, it most likely comes from a simplified script of et, Latin for “and”, but nobody really knows why.

Algebraic notation to define operations was strongly promoted by the Andalusi mathematician Alī al-Qalaṣādī in the 14th century, where each sign was represented by a letter of the Arabic alphabet —for example, ﻝ for ya‘dilu (meaning “equals”). But it was actually a Welsh mathematician, Robert Recorde, who coined the modern equals sign (=) in the late-16th century. By that time, Europeans were mapping coastlines beyond Europe and the Mediterranean, Copernicus was posthumously publishing his Revolutionibus and the printing press was spreading like powder all over Europe —and people were still tediously writing “is equal to” or aequale est in Latin instead of just “=”. Try to make our kids do mathematics that way and see how long they can hold!

To be fair, most of the notation was standardised by the 20th century in the context of mathematical fields like set theory, groups, graphs, and others that most readers would not be familiar with. In fact, the evolution of mathematical notation and the stages at which one learns it in the educational system are uncannily correlated.

By primary school, around the planet, one learns the first symbols standarised by the 16th century +, −, =, ×, ., √ , ( ).

By mid-high school, one would learn the rest that can be easily written on a modern keyboard or a calculator with one or two keystrokes: ·, ⁄, %, <, >, ∞, ≠, xy , º, cos, sin, tan. These were developed by mid 17th century.

Once one goes on to study sciences in upper high school, one comes into contact with integrals, differentials, functional analysis, binomials: \int, \partial, x', f(x), \sum, \binom{N}{k} = \dfrac{N!}{k!(N-k)!}. These examples have linguistic roots too, but also “famous personalities” for example Newton’s binomial —Newton was known to have anger issues, that might explain the exclamation mark (!), though it was developed by Christian Kramp. More seriously, Newton’s arch-rival of all times, Leibniz thought that having the right notation was the solution to all human problems —if humans could create a universal logical language, then everyone would be able to understand each other. In the case of mathematics, Leibniz actively corresponded with his peers at the time to convince them that notation should be minimal. That, in fact, has informed most of our modern mathematical symbolism. Going back to our tedious exercise, this decision on minimalism might have a cognitive reasons, human operating memory is limited to about 3 to 5 items, and this storage lasts only few seconds, so it makes sense to develop notation that allows computation and arithmetic to fit well in that memory space. These symbols were common use by the early-19th century, though some, like \int, \partial by Leipzig were developed earlier or at the same time as the signs ·, ⁄ —these two being simplifications of the product and the division. Many of these symbols cannot be easily typed from your keyboard and need special code to type or display.

By the end of a technical degree like engineering or physics, one gets to know most of the mathematical notation developed by the mid-20th century, with scary things like tensors written using something called Einstein Notation: \Gamma^{i,j}_{k} —Einstein was known to be bored easily, that might explain that he preferred the simplified notation to the degree that dyslexic minds like mine mix these little indices.

Beyond these, one enters into advanced or specialised studies to learn the fancy ones: \rightarrow, \Cup, \exists, \forall, \vdash, \because, \therefore. Many of these are just substitutions of words that are mathematically “conceptualised”, like the numbers. For example, the Braille-looking \because, \therefore are just symbolic representations of the verbal statements “because” and “therefore”, respectively. Many of these symbols were developed during the late 19th to late 20th century. The most avid use of signs is in the field of mathematical logic, where Peano–Russell notation informs some its rules —Russell was a known geek, self declared to know nothing about aesthetics, that might explain his dislike of using words, which have the tendency to change meaning. Funny how he did not write much about the mostly aesthetical music, which has also a standarised quasi-universal notation, as we will see.

In short, in standard regulated education, one progresses through about 100 years of mathematical notation history every two or three years of modern study —although that is a non-linear accumulation. As one enters logic and set theory, the number of symbols needed run into the low hundreds.

Symbols by approximate “popular” introduction date

Nevertheless, the point at hand with mathematical operational notation is that it took hundreds of years to adopt the standardised form that is now widely used in all the teaching systems around the world. That evolution and standardisation did not happen in isolation, but were interwoven with other branches of knowledge, mainly technical ones. These technical fields needed the rapid adoption of simplified standards that could be learned efficiently by a specialised community of experts. This process can be understood, in part, in a similar way to how linguas francas are constructed —from a simplification of an already existing language— to be the means of exchange and understanding among a subset of people from many different cultural backgrounds who share similar conceptual and material items.

This notation is nothing new by itself. It is just a reflection of human needs —mutual semantic undertanding around a limited subset of concepts— and practical solutions that might have some cognitive biases. What is new is the fact that this notation reached a planetary scale. As we have seen with the spread of communication, that process is just a matter of scale, not of quality. But, in my view, that global scale makes all the significance and sets the question of this book. Mathematical notation, and its quasi-universal use, shows one paradigmatic example of how we arrived there. How we arrive there, or not, and a standard is kept regional, is significant.

Mathematical notation has been the first of such lingua francas to become a standardised language used across the whole planet. It is, however, limited to be used only by someone who needs to do arithmetic —which, in our case, is anyone who has entered a regulated educational system. As we will see, regulated educational systems have reached over 80% of the human population, and are implanted in virtually every new human being born.

Now we have the example of how a truly global language —albeit a limited and specialised one that rides on the back of the universality of what it studies— is created, adopted, and made universal. In particular, this one has been made universal without any clear agreement or premeditated guidance, but rather by the sheer pressure of technical needs and the dominance of Western knowledge systems. Same as with time keeping. Time-keeping, by the way, will come back, and we will see that the universality actually is held by technical needs, mostly as a matter of sailing ships, driving trains and flying planes around the world while knowing where you are also in space.

So, the World has not finished with mathematics as universal communication, other technical and symbolic language are coming. The Metric System is coming, and this time, with bureaus.

Previous

Time keeping

Next

Francas, Linguas Francas

Time keeping

Posted on by wanderer

One interesting predecessor to unified measurement and standardisation is that of time. Most people might not be aware how puzzling it is that, as of now, across the whole planet we share a common timekeeping system spread throughout most societies of the world. When you look at your watch, you see it divided into 12 or 24 segments, denoting hours, and each hour is divided into 60 units, called minutes. Again, each minute is divided into 60, and we call that division a second. None of this is new to you, but what should surprise all of us is that it is not surprising for most people on the planet! And that’s just it—seconds are the basic unit of measurement of time across the entire world. Why, and how this fact came to be, is not a given. In fact, timekeeping is an extremely aberrant, arbitrary, and silly system if we compare it to the more common numerical system in divisions of 10 (we will see the metric system later on). Why aren’t there 100 seconds in a minute, 100 minutes in an hour, and 10 hours in a day? We could all stop dividing by 60! Our system seems complicated, and it’s not only our adult selves that feel so. My father, who has worked in the educational system all his life, told me that children learn the decimal system quite quickly; however, it takes them much longer to internalise timekeeping. You might have experienced this difficulty yourself as a child, or seen it in your own children if you’ve raised them. Then why does this strange and somewhat difficult system not only exist but is also the same everywhere? Didn’t other parts of the world create different timekeeping systems that made more sense? Why are these no longer around? As we will see, in large part it is because our current international timekeeping standard comes from one of the oldest measures.

Timekeeping is quite common across cultures—perhaps it is a human universal. The easiest division of time is into days, as it is a cycle that dominates all our actions in life, especially our sleep cycles. The next division of time across cultures is usually the cycle of the moon. About 29.3 days have to pass for us to see the moon in the same phase and position in the sky. This moon cycle gives us a close approximation to our current month lengths of 30–31 or 28–29 days. The third rhythm that many cultures pick up on is the annual cycle of the Earth orbiting the Sun. For higher latitudes in both hemispheres, that annual revolution—together with the tilt of the Earth’s axis—gives strong variations between seasons. Days become noticeably longer and shorter along that rhythm, and the weather and natural world follow these changes, with cold during the short days, and heat during the long days. In tropical latitudes, where the variation in the length of the day is not as pronounced, the coming and going of the rainy seasons usually plays a similar role to the cold and hot cycles. In short, most humans around the planet adopted these three naturally occurring cycles as the basic units of time division. When combining the Moon and Sun cycles, this gives us the numbers 12 and 13—i.e. the number of lunar months in a solar year. But this concerns the calendar more than the clock.

We have two main methods of temporal measurement: the calendar and continuous timekeeping, which could in principle be independent of natural cycles. But the calendar is a kind of timekeeping and has given us two numbers to play with. The number 12 is prominent in many counting systems; it even has a specific name in English: a dozen. The number 13, not so much—it is even seen as a “bad luck” number in some cultures. Why is 12 popular and 13 hated, then? This difference is also due to boring calculus. It is easy to divide 12 by 2, 3, 4, and 6. Try doing that with 13—any luck? If you remember your prime numbers, 13 is one of them—only divisible by 1 and itself. Probably, most nerdy ancient people who had to do the tedious task of measuring time preferred the “neat” 12 instead of the unfriendly 13.

But why 60, then, for continuous timekeeping on a watch or clock? Why the 60, 60, 24 division?

We need to start talking about the Babylonians, and how they counted. How do you count using your hands? Most of us would count the number of fingers on each hand, up to 10. But one can increase the amount that can be counted by using the phalanges in each finger. If you count them on the four longer fingers of one hand, that gives you 12—once again this neat nerd number derived from solar and lunar cycles. Then, what better number to divide the daylight hours than 12? But there are an equal number of hours in the night (in equatorial regions), so the number of hours when the sun is out is roughly the same as when the sun is away. If daylight is 12 units and night is 12 units, that gives us the universal 24 divisions of the day: the infamous hours.

Then the 60. Going back to the Babylonian counting, if you count a dozen on, say, your left hand, and on your right hand you keep track of the number of dozens by flexing one finger each time, that gives you five dozens—or a total of 60. If we divide that hour into 60, we get the infamous minutes. The punchline, however, is that despite the importance of 12, the Babylonian sexagesimal system was based on six groups of ten, not five groups of twelve! In any case, that sexagesimal system is the basis for the 60 divisions—or hexagesimal—which the Babylonians also used to divide a circle into angles, another of the universal measures we will examine.

Why the infamous seconds exist, and are simply 60 divisions of a minute, is not such a clear story. Why wasn’t it a division of 10, or 100, or 24? The subunit of a second—a millisecond—is divided into 1,000 units, so 60, although used to define the minutes from an hour, had no need to be used again. What might explain the 60 seconds is another natural unit, quite random at that: the standard resting human heartbeat. If you measure your heartbeat after a period of rest, or just after waking up, there is a high likelihood that you’ll have just over 60 beats per minute.

However the infamous seconds really came to be, the Babylonians standardised them, and due to their central location, vertebrating the Africa–Eurasia connection, seconds, minutes, and hours spread. The large-scale societies around Babylon—such as Egypt, the Greeks, one of their successors Iran, and the polities of the Indian subcontinent—adopted the Babylonian system early on. Crucially, it spread to all the European nations, who then forced it into the administrative apparatus of their colonies, which, as we have seen, covered most of the planet. Even the Chinese adopted a version of the Babylonian sexagesimal division when the Ming dynasty commissioned Xu Guangqi in collaboration with the Jesuits to adapt the Gregorian calendar and timekeeping to the imperial system. Although this reform was only officially adopted during the Qing dynasty in the mid-17th century, it was partly influenced by the Jesuit Johann Adam Schall von Bell and his improved methods of predicting eclipses. Astronomy, we must remember, was deeply linked to astrology in both European and Chinese courts, and astronomers performed the functions of astrologers in advising rulers.

Calendar

Concerning the universality of the Gregorian calendar, it also seems a convoluted, silly, arbitrary system. Why are some months longer than others? Why is your birthday on a Tuesday one year and on a Friday another? There are vastly superior calendar systems out there. Though, some of these alternatives tend to require the addition of a 13th month and a bizarre annual “blank day”, which doesn’t go on the calendar at all. We just chill out, have a holiday, and pretend it’s not there.

The Gregorian calendar has a complicated and protracted history. All the successors of the Roman Empire, and the Christian churches, used the Julian calendar until AD 1582. The Julian calendar, as the name suggests, comes from the Julius Caesar. He borrowed it from the Egyptians and imposed it on the Roman Republic as a more stable alternative to the Roman system. The Catholic Church adopted the Julian calendar at the First Council of Nicaea in AD 325. However, Christians had conflicting ideas on how to celebrate Easter, and it took nearly half a millennium before most Christians agreed to follow the Nicaea rules. In the Egyptian calendar, once every four years a day is added to February. That’s the year when February has 29 days—and some people still joke that those born on that day don’t get to have birthdays.

The problem with adding one day every four years is that, after a few centuries, it messes up the seasons—meaning that the spring and autumn equinoxes, and the summer and winter solstices, begin to drift on the calendar. By the 16th century, this was still a minor issue (only ten days had shifted in 1550 years), and it didn’t seriously affect agricultural practices. However, the motivation for change was religious: the Catholic Church was concerned that Easter might not be celebrated in accordance with the scriptures. Easter follows a lunisolar rule, which causes the date to shift every year: it must occur on the first Sunday after the first full moon of spring. This meant that, technically, Easter could end up being celebrated in winter if the calendar drifted too far—risking some sort of cosmic blunder. It wasn’t equally important for all Christians, as many Eastern Orthodox churches still follow the Julian calendar.

Some sectors of the Catholic Church pushed for reform early on. In the late 15th century, the man chosen to oversee it was a German mathematician with the wonderful name Regiomontanus (Latin for “royal mountain”). Unfortunately, he died before the reform could be implemented. A century passed, during which all the Protestant wars took place. In the aftermath, a diminished Catholic Church finally agreed to set the new calendar—approved by Pope Gregory XIII, who gave the calendar its name. But the Pope could only set the liturgical calendar for the Church. The civil calendar—used by governments—had to be adopted by each administration. Moreover, the emerging Protestant denominations were deeply sceptical of anything coming from the Pope and were not eager to adopt a “papist” invention, even if it made sense. The Puritans even tried to ban Christmas for being too Catholic.

Nevertheless, Catholic powers and administrations such as the Polish–Lithuanian Commonwealth, the Kingdom of Spain (which then included Portugal and most of Italy), and France, as well as their colonies and dependencies, adopted the Gregorian calendar as their administrative standard. Parts of the Netherlands under Spanish control (now Belgium) also adopted it; the rest of the United Provinces followed over the next few decades. So did the Holy Roman Empire, including Austria, Hungary, Bohemia, and many of the German states.

Some Protestant nations, like Denmark and Sweden, also adopted the Gregorian calendar relatively early. Though Sweden did so in a somewhat chaotic way—switching to the Julian calendar, then to the Gregorian, then back again, and finally settling on the Gregorian in 1752, the same year Britain and its colonies adopted it. To avoid referring to the Pope, the British called it “An Act for regulating the Commencement of the Year, and for correcting the Calendar now in Use”. For years, Swiss towns just a few kilometres apart had calendars ten days out of sync—allowing people to celebrate Christmas or Carnival twice in one year!

Later on, Eastern Orthodox countries such as Greece, Serbia, and Russia adopted the Gregorian calendar for civil purposes, though many retained the Julian calendar for liturgical use—or switched to the “New Julian” calendar, making things even more confusing. This is why people in Moscow celebrate Christmas on 7 January (in the standard Gregorian calendar). Others, like Ukraine, have switched to the Gregorian calendar entirely.

The Gregorian calendar is now the de facto global calendar—though it was never formally agreed upon. Administratively, all European countries and their colonies adopted it. Even the Chinese, as we’ve seen, integrated it into imperial systems. Of the few non-colonised countries, only Nepal, Afghanistan, Iran, and Ethiopia still use different civil calendars. Others like Japan, China, Thailand, and Saudi Arabia eventually adopted the Gregorian calendar for administrative purposes—Saudi Arabia only doing so in 2016! Some of these countries still use different systems for counting years or determining the New Year, but their months, leap years, and weekdays follow the Gregorian calendar. In many places—such as the Orthodox Christian and Muslim worlds—two systems coexist: one for liturgy and another for administration. Only Iran’s Solar Hijri calendar, or Shamsi, is more astronomically accurate than the Gregorian. It sets the start of the year to within a second of the spring equinox on Iran’s standard meridian at 52.5° East.

Finally, most international institutions—the United Nations, the Olympics, global research networks—use the Gregorian calendar, reinforcing its role as the de facto global timekeeping standard. Timekeeping—both in hours–minutes–seconds and in calendar form—illustrates how ancient measurement systems, copied or adapted from long-gone administrations like Pharaonic Egypt and Babylon, are still with us and have become near-universal norms, despite never being formally imposed on the entire world.

Later we will see that something like “timekeeping” is not so unquestioned. And that this seemingly universal but rule-less agreement on time has also undergone standardisation—and even the creation of global institutions, as we will see in the case of standard time and the truly infamous leap second—imagine scary quotes. Like the second, double globals, in use and in institunionalised, is what we will need to pay attention to when asking these texts question.

Previous

Commerce – Mercantalisation

Next

Mathematics, universal not the way you think

Revolutions, Scientific Revolutions

Posted on by wanderer

The peoples that embarked and supported the exploration of new trading and colonising routes soon discovered that the free-riding of the technological advantage could be easily perpetuated. Thanks to that, the ones that invested in better and faster understanding of the world, plus the technical innovations that that understanding and implementation represented, contributed to a further control of the world’s connectivity. From that on, there were no major barriers to a hyperconnected world. What they could not control by exchange, they would control by overpowering, as the conquest of Malacca, the Aztecs, the Incas demonstrates. If you kept on expanding your technological and resource allocation dominance over other peoples, your system would be the one to dominate, and that’s exactly what the Western nations did over a period of a few centuries.

New trading routes led to an excess of wealth that could be poured into more navigational sophistication, which in turn would make the trading networks more reliable and affordable, freeing more resources for further improvement. Part of these resources went to the birth of modern science, changing forever the way our understanding of the world was established.

To make a boat sail safely from port to port you would rely less and less on divinity and more on your instruments, navigational skills, the capacity to understand the sky, star positions, read the winds, proper sails, masts, ropes to withstand storms, carrying lemons to stop scurvy, social structures to govern a ship and stop mutinies, etc. Those powers that would put scientific knowledge to good use would have in their hands better control of the high seas and the peoples cruising them. Likewise, those who understood better the fabrication techniques could build better vessels, and equip them with better weapons. On the other hand, the faraway encounters would contribute to the scientific understanding of the world, like sea currents, Volta do mar, steady trade winds, or even catamaran technology from the Pacific and front crawl swimming techniques from North, South America, or South Africa.

In fact, Columbus’s error regarding the radius of the Earth (which he was convinced until he died) was due to the preliminary stages of scientific knowledge attempting to describe the world we lived in. In that case, he was mistaken, but the geographers’ community soon recognised the error and corrected it (or lent more credibility to other estimates circulating at the time). This iterative process helped to better understand the world that was opening up before them as they tried to cartograph the new routes faster than they were explored.

From these explorations and shocks to the perceived worldview, it is not difficult to imagine that the notion of an entire landmass the size of the Americas suddenly appearing on maps (over about 20 years) might have led to the acceptance of rethinking the entire Universe. If the Earth contained a whole part of itself that was unknown to the Old Scriptures, how much more knowledge might be out there—waiting to be found, explored, and understood—not through the lens of the Scriptures, but through the lens of something new? These cartographic shifts might easily have been the seeds for scientific enquiry—the seed of the Scientific Revolution.

In fact, it is interesting to reflect on that word, “revolution.” What does it stand for? It comes from the root “to revolve”, which means to spin around. Why—if an entire continent had been missed, and Jerusalem is not the centre of the Earth—could it not be that the Earth is not the centre of the Universe either? That kind of thought might have helped Copernicus push the heliocentric idea: that the model best suited to describe the Universe is not a geocentric one, with the Earth at the centre, but one with the Sun at the centre of the known cosmos. Copernicus was not the first to propose that idea; the Pythagoreans had already supposed the Earth might move, and Aristarchus of Samos proposed a heliocentric model in the 3rd century BCE. Seleucus of Seleucia said something along the same lines in the 2nd century BCE. About 600 years later, in the 5th century, Martianus Capella, from Roman Carthage, proposed that Mercury and Venus spun around the Sun. At about the same time, Aryabhata in Patna, India, proposed that the Earth spins and that the planets orbit the Sun. In the 12th century, Ibn Rushd (Averroes) and Nur ad-Din al-Bitruji of the Cordoba Caliphate were also critical of the geocentric model and proposed alternatives. Their views spread into European intellectual spheres. However, none of these theories gained much traction at the time they were proposed. One can say that the mindset of the people of those generations was not particularly open to such a shift in worldview, nor was it needed for any practical purpose.

To be open to other worldviews becomes more likely if a sweeping 30% extra landmass is literally put on the map. The same world that the Scriptures plus Classical Philosophy were so certain they understood. Even though the Catholic Church did not pay much attention to the fact that the world was different than said, surely minds would become more open—even if obtuse. Moreover, those same conceptualisations ended up making navigation more precise. And the required navigational observations and technical means (star and planet positions, astrolabes, compasses, telescopes, clocks…) helped to question the worldview in a more rigorous way—with the newly discovered facts holding more face value than old beliefs. In short, cosmological views came to serve a practical purpose.

Therefore, the landscape was set. After Europeans became aware of a New Continent, Copernicus was able to push his idea (initially as a short leaflet in 1514), and later publish, after his death, his De revolutionibus orbium coelestium. His heliocentric model was not the one we know today. Copernicus’s model was not that innovative, nor significantly simpler than the Ptolemaic one, because he still needed the use of epicycles (small circumferences around the circular orbit of the planets) to accurately describe the rotation of the planets around the Sun. It would be Kepler—about 70 years later—who, after throwing out his own Mysterium theory of planetary movement because Tycho Brahe’s observations did not match, solved the motion of objects in the Solar System with simple elliptical orbits and delivered us pretty much the view that we now have.

Even after the heliocentric vision of the World was presented, the conviction of perfectly circular orbits was not abandoned, here a drawing trying to explain the elliptic orbit of the moon (Luna) around the Earth (T) with three epicycles. Calculations according to Schöner’s Tabulae resolutae and Reinhold’s Prutenicae Tabulae in lecture notes from 1569

The difference with all the previous scholars—after Copernicus’s posthumous publication—proposing that the Earth was not static, was that the public at the time was much more accepting of the revolution of the Earth thought. A thought that would be revolutionary!

Revolution, at the time, had the meaning that Copernicus used in his title: simply the spinning around of the celestial bodies—how they revolved around the Sun. Revolved, revoluted, revolution. It was a physical description, like that of the revolutions or cycles of an engine, or as one famous revolutions podcaster puts it, “coming full circle”, just to come back to the beginning. Revolution did have, on rare occasions, the meaning of change prior to Copernicus’s work. However, the acceptance of heliocentric theory by the public of the time. It was so disruptive to the mindset of the age, overturning millennia of knowledge and worldview—so Earth-shattering (pun intended)—that the first main word of the work itself, revolutionibus, was adapted less than a century later to mean the overthrow of a political system (the Glorious Revolution in Britain). When transferring the physical meaning to the political one, revolution meant “a circular process under which an old system of values is restored to its original position, with England’s supposed ‘ancient constitution’ being reasserted, rather than formed anew”. At that point the use of the word was far form the meaning that it has now, as a radical new direction, or changing of course of what was before. Soon after, however, the word gained the modern concept of revolution, as used for the French one, which probably someone has heard about. Now revolution is more widely understood as the shattering of a previous political, social, technological—or otherwise—system, and the establishment of a new one: the Glorious Revolution, French Revolution, Industrial Revolution, Agrarian Revolution, Sexual Revolution…

It could be that the people at the time—after the Earth had been kicked aside, given rotation, put in orbit around the Sun, and the stars made still—experienced a mental shift so profound that it allowed for a reshuffling of many pre-existing mentalities. Maybe it can be compared to the shattering effect, almost a rite of passage, that many children in the Western world experience when they realise that Santa Claus is not a real being, but a construct created by society to make them believe that the bringer of presents is this exotic figure from faraway lands, and not their parents or families. For the child, it is already a big impact—and if you experienced that, you probably remember the moment, even if it was decades ago. Then imagine if instead of just one child at a time, it were an entire society realising, more or less simultaneously (within a generation), that the reality they had so strongly believed to be true, no longer was. That is what the so-called Copernican Revolution brought to European thought in the 16th century: a collective, mind-shattering effect. We, as humans, have been toying with these moments ever since. But more about that later.

In fact, the public that was more open to these ideas was also in the midst of another revolutionary movement, which at the time was called a protest, for lack of a better word: Protestantism. If the world, the solar system, the Universe, the Cosmos, was not as the Church claimed—with extra continents unaccounted for, the Earth in motion, and stars being other suns, perhaps with other Earths—then the Church became open to protest and reform. And if protest and reform were possible, then the acceptance of truly exotic ideas—like the Earth revolving—became easier in a society already undergoing profound transitions. In fact, different solar system models were readily adopted by Tycho Brahe and Johannes Kepler, Danish and German astronomers sponsored by Protestant-friendly kings. Meanwhile, Latin astronomers such as Galileo Galilei and Giordano Bruno had major conflicts with the Catholic Church in Northern Italy—Galileo famously tried, Bruno burned at the stake. Bruno’s seven-year trial and sentence to be burned alive was not specifically for his belief that the stars in the sky were other distant suns orbited by other planets, but also because of his rejection of most Catholic doctrines.

The difference between Copernicus in the 16th century and all those who proposed alternative cosmological systems before might be that society was more open to new ideas because of empirical slaps in the face—steadily, repeatedly, forcefully. First, sailors and their investors realised that direct observations could actually shift reality—such as the discovery of a continent, accurate measurement of latitudes and longitudes, and the real size of the Earth’s circumference. Second, astronomers and their sponsors (who were often astrologers for European courts—better predictions meant better horoscopes; the zodiac pays for your smartphone, if you think about it) found that when your health or the outcome of a war depends on the conjunction of Saturn and Jupiter, and your astronomer looks through a telescope and tells you that these planets have rings and moons orbiting them, you might predict better when to wage your next war. Third, traders could more precisely calculate profits or invest in new products—like new dyes and pigments (e.g. scarlet), or learning how to plant species such as pepper, potatoes, tomatoes, tobacco, coconuts, sugar cane, among others, across the world. Actual measurements began to overturn established doctrines one after another; these facts reinforced the critiques of the old system and laid the foundation for an alternative system of establishing knowledge. The Scientific Revolution went hand in hand with the development of better instruments and measurements that define the modern world we experience today.

It was equally important that these new ideas travelled and multiplied faster than ever before. On one hand, naval interconnectivity regularly reached all continents and the major inhabited landmasses of the planet. From there, peoples—willingly or unwillingly—became part of a shared system of exchange, a process that continues today, where nearly every human being is regularly connected to the rest of the world in one form or another. Our present hyperconnected world is extending the reach and frequency of connection to ever more remote places. On the other hand, the printing press allowed for the multiplication of ideas at a rate faster than authorities could suppress them. Even if the works of figures like Copernicus or Bruno were censored, confiscated, destroyed, or burned, it was much more likely that one copy would escape, be read, and be copied again. Before the printing press, Protestant ideas—like those of the Hussites in the 15th century—did not spread far beyond their place of origin (e.g. Bohemia). Later, Prague—with its famous astronomical clock—would host Brahe and Kepler. On the other end of the chain, at the point of reception, Spanish missionaries actively protected indigenous languages (while simultaneously suppressing their cultures) in regions such as Mesoamerica, the Andes, and the Philippines, to prevent indigenous peoples from being exposed to “dangerous” Protestant, Enlightenment, or revolutionary ideas. To this day, these regions preserve some of their linguistic diversity and remain heavily Catholic, with the Philippines being the only nation (alongside the Vatican) that does not permit divorce.

Our hyperconnected and idea-copying world is the one that gave birth to the concept of humanity—a “humanity” that can now begin to ask itself what it wants to do, now that we have the means to communicate with one another, and the resources (or energy levels) to invest a fraction of that energy in specific goals. But before asking that question, we first need to understand the mechanisms by which a hyperconnected people is able to pose it: which networks are activated, in which language communication occurs, with whom that exchange is implemented, and what actions can—or cannot—be taken. What is the agency?

Curiously, one of the early adopters of Copernicus’s thesis was Thomas Digges, who removed the need for the sphere of fixed stars. He proposed the existence of distant stars scattered throughout the Universe. This led him to raise the paradox of the dark sky: in an infinite Universe filled with stars, the sky should look like the surface of the Sun, because in every direction there should be at least one star. Since the sky is black, the Universe cannot be infinite. With that in mind, the Copernican Revolution—which displaced us from the centre of the Universe—is still not complete. It is geographical, but not temporal. Heliocentrism kicked the Earth and its peoples out of the centre of space, but the dark sky placed us in a special time—a time when we can still see the horizon of the visible Universe. Now we are in another special time—the time when humanity is conceptualised. The time to ask: what does humanity want?

Previous

From the neighbours to the oceans

Next

Western dominions

Collaboration

Posted on by wanderer

Another important behaviour that humans share with many animals is socialisation and collaborative action. This is observed across a wide range of species, including not just animals but also organisms from other biological kingdoms. There are many examples of this collaborative behaviour.

Cetaceans (whales, killer whales, porpoises, and dolphins) engage in social collaboration to achieve common goals, such as developing feeding strategies and defending against aggressors. A species that is particularly close to us in terms of social behaviour is the wolf. Wolves form small packs of up to forty individuals, working together for survival. Their domesticated relatives, dogs, are also highly social animals capable of interacting with many other species, especially humans, to a remarkably sophisticated degree. This is exemplified by cases where humans have been effectively adopted by dogs, such as in the myth of Romulus and Remus—the legendary founders of Rome—or in more recent historical accounts like that of Marcos Rodríguez Pantoja. Marcos lived among wolves for 11 years after his father sold him to a landowner who entrusted him to a goat-keeper, who later died. Marcos recounted:

“One day I went into a wolf den to play with some puppies that lived there and fell asleep. When I woke up, the wolf mother was cutting deer meat for her puppies. I tried to take a piece from her because I was also hungry, and she swiped at me. When she finished feeding her puppies, she looked at me and threw me a piece of meat. I didn’t want to touch it because I thought she was going to attack me, but she kept bringing it closer with her snout. I picked it up, ate it, and then she came up to me. I thought she was going to bite me, but instead, she stuck out her tongue and started licking me. After that, I was already part of the family. We went everywhere together.”

Marcos also recalled that after reuniting with his father, his father simply asked him for the old jacket he had left behind.

If we extend the concept of collaboration further to include infrastructure, we see that insects and arachnids also exhibit highly cooperative behavior, forming vast colonies. However, these types of social structures are not exclusive to invertebrates; similar cooperative infrastructure-building can be observed in birds, beavers, and many mammals that create dens. In the case of insects, some colonies function almost as single superorganisms, with specialized individuals performing specific tasks or switching between roles as needed. Other social animals, such as meerkats, also have fluctuating specialized roles within their groups, such as caring for the young or standing guard to raise alarms against predators.

For social arachnids, as well as some bird species and most den-dwelling animals, collaboration seems to be primarily focused on building communal nesting or feeding structures. However, outside of these specific activities, they tend to act as individuals.

On the looser end of social structures, we find schools of fish and herds of various land animals. These groups function as dynamic, collective entities where decisions about feeding, protection, and movement are made communally.

Expanding the concept of socialization even further, we can consider co-dependent ecosystems. In such ecosystems, plants and animals—or even plants with other plants, bacteria, and fungi—are so interdependent that they cannot be considered separate entities. Biologists refer to these relationships as symbiotic or, in cases where one organism is significantly larger than the others, as holobionts. A common example of a holobiont is the relationship between a human and their gut bacteria, whereas an example of symbiosis is lichen, which is formed by the mutualistic association between fungi and algae.

The scale of communication and collaboration in most living organisms is usually limited. For example, some ant species form supercolonies containing trillions of individuals, such as the Argentinian fire ant supercolony (Linepithema humile). These supercolonies cooperate with genetically related colonies while competing with unrelated ones, allowing them to dominate newly colonized lands by leveraging globalization. However, despite their vast numbers, their communication networks remain limited to neighboring colonies and do not extend much further.

In contrast, human collaboration is, in principle, boundless. Even in the Palaeolithic era, commercial networks facilitated the exchange of materials over vast distances—hundreds or even thousands of kilometers— with materials transported almost 200kms at least as early as 45,000 years ago. This scale of mobility far exceeded that of individual bands and their immediate neighbours. No other species exhibits such an extensive range of cooperative behaviour.

Even among our closest extinct relatives, there is uncertainty regarding the extent of their social networks. Recent genetic research has shown that a group of Neanderthals remained genetically isolated from neighboring groups—less than a ten-day walk away—for more than 50,000 years. However, this genetic isolation is not unique to Neanderthals. Studies suggest that modern humans, too, have lived in genetic isolation from neighboring communities for tens of thousands of years. For instance, the ancestors of African Pygmy foragers are believed to have diverged from other human populations around 60,000 years ago, though they intermixed more recently in several occasions.

Intelligence <- Previous Next -> Communication

Previous

Intelligence

Next

Growth of communication- Culture

Intelligence

Posted on by wanderer

Starting with behavior that can be understood as intelligent, we can focus on tools. These were already present in the Homo lineage and are also shared with many other species on this planet. We can understand tools as macroscopic external elements of an animal’s body that are used to gain access to more resources, security, and reproductive success. More conceptually, tools can also be strategies to achieve the same objectives without the use of any specific external object, other than perhaps geography.

The use of tools can be both learned and innate and is abundant in the animal kingdom. Examples of tool use range from primates using stones and branches to crack nuts or open coconuts, to birds creating complex fishing utensils with their beaks and claws, especially in the family of Corvidae (ravens and crows) and psittacines (parrots). Dolphins, for instance, use the shore or each other to trap their prey.

But tool use can extend far beyond what we would usually consider “intelligence.” For example, creating nests and structures to attract females (as seen in bowerbirds), ants using sticks to build bridges or using fungus to ferment food, chickens eating rocks to aid digestion, hermit crabs using shells and plastic cups, caterpillars using leaves to make cocoons, foxes building dens, and beavers building dams. One could consider these behaviors as simply “innate” tool uses. However, there is ample literature arguing that the “social learning” of animals, whether innate or learned, is difficult to define and differentiate. Although instances of problem-solving behavior spreading have been observed, such as parrots opening trash bins in Australia.

Interestingly, the spontaneous use of tools—using environmental elements for one’s own benefit—is probably widespread in the animal world. Individuals of many species use tools in controlled lab environments, where they can solve complex puzzles using elements of the system. For example, pigs can play video games, rats solve mazes, and squirrels solve puzzles.

However, despite the shared use of tools among many animal species, we are fundamentally different. This shows that “intelligence,” in the case of humans, might be necessary but not sufficient to explain why we are the way we are. The key difference is culture. Many of the previous examples of animal innovation do not constitute culture. This is because the discoveries of one individual are often not explained or described to fellow individuals of the same species. In the case of puzzle-solving and tool-making, each individual must solve the problem themselves initially, which is an inefficient way of obtaining resources. Not all individuals of the same species show the same dexterity in solving the same puzzles, as we will see in more detail with the case of Mango the crow.

There are examples, though, of chimpanzees who learn from imitating fellow chimps or human instructors on how to open a complex box to obtain food or learn sign language. However, when imitation experiments have been conducted with both chimps and humans, it has been observed that humans tend to repeat every step of the process, even futile ones that do not contribute to obtaining the reward, this seems to be in the contest of our brains being wired for costly rituals, even at a young age. On the other hand, chimps, once they learn which steps are necessary, tend to avoid the unnecessary steps. This indicates that chimps are actually more efficient in problem-solving than humans, avoiding unnecessary steps. However, it also points to the fact that humans are better at copying than our closest relatives, to the point that, even understanding the mechanics of something, we keep extra steps for the sake of reproducibility. Although some dispute these conclusions.

Opening <- Previous Next -> Collaboration

Previous

Opening

Next

Collaboration

Science and Mountaineering

Posted on by wanderer

image

I guess this has to be discussed because of how the current research methodology affects to many young scientist.

I would dare to say that one of the main reasons that many people enters research is because they want to discover something new.

Then I’ll compare that to climb a mountain, bur not just any mountain, but one that you don’t know how it is, where it is, or if exists at all!

Then how shall proceed someone that has only theoretical knowledge in mountaineering and has done a couple of treks in hills (a fresh graduate)?

Well that’s difficult. One would like to climb to climb the Everest, as the famous saying goes, because is there! But climbing the Everest is not easy, and worst, it has already been climbed…

So what the supervisors want you to do? well, get you  in shape so you can be a Sherpa to carry on helping them climb.

And what they want you to climb? certainly not something that is not known how it is, and even less something  you don’t know if exists at all.

What any sensitive person would do is make you climb something extensively surveyed, that has a clear path and peak (goal) and that might have been climbed already, but in a different way.

That’s sensitive, then many supervisor can be, well, not sensitive…

And then for the aspiring mountaineer that might seem dull and purposeless. What’s the reason to climb something known if there are many exiting mountains out there untouched?

Well the thing is both are right and both are wrong.

It is right to train
One one hand, First you shall be prepared, and the difficult part is that depends on the mountain it might take more or less effort to get on shape (skills), and you might need more or less people on shape and specialized roles to get there (teamwork).

Otherwise you will fail or get lost, which is a nice way of training too, but difficult to justify to a funding agency. 

Second lets be realistic, not everybody can climb a brand new mountain. Most of mountaineers keep climbing the same ones, maybe in slightly different ways and times. Still I know some that keep climbing unclimbed 6000ers :D.

Therefore  you shall not be frustrated if you never claim a new one, unless you REALLY want to climb an unclimbed one.

It’s right to try
So, on the other hand, first if someone is really motivated you shall not waste the energy, determination and motivation of these by doing dull hike or sherpa work. What one might lack on skills can be compensated by pure determination,  confidence, fearless and instincts that might be different for a young unweathered mountaineer.

Second, it’s good too let the determined try and encourage and help them instead of the opposite. It’s a nice bet that in the worst case might end in failure but in the best you might climb or discover that mountain! Since it’s a unknown one maybe even one inexperienced mountaineer can clam it, as the skills required might also be something original.

It’s worth the try, at least for some part of the time.

Creativity not encouraged
Unfortunately the way I see science now I would say that creativity is not encouraged, to be the least pessimistic. That limits the exploration capability.

Confidence
That’s what most seems to be about.
If you are confident that’s what will push you to struggle trough. If you are confident you can attempt the unknown. If you are confident and motivated  you will push against any hardship to find the way.

But what brings confidence? Well in this system it is the most dull of things, marks for fresh graduates, and number of publications for seniors. Hardly something to attempt crazy endeavors.

What shall bring confidence is skills and encouragement in breakthrough thinking.

Yeah, not all the time, not blind encouragement, but hell we are scientists, we shall find a better and more engaging way of exploring.

What is stopping the encouragement  then?
Many things, the ones that can be changed are the expectations of having a publishable outcome, and all the funding system and CV building. What hardly can be changed is the complexity and difficulty of pushing new frontiers and the need of highly skilled and specialized labour for that.

One way forward?
Since the world out there is so big, there shall be room to create a system that pushes the dreamers and explores to brand new fields, and the hardworkers and skilled to expand the old ones.

There is a wold out there, let’s be wise in how to climb it 😀