universal

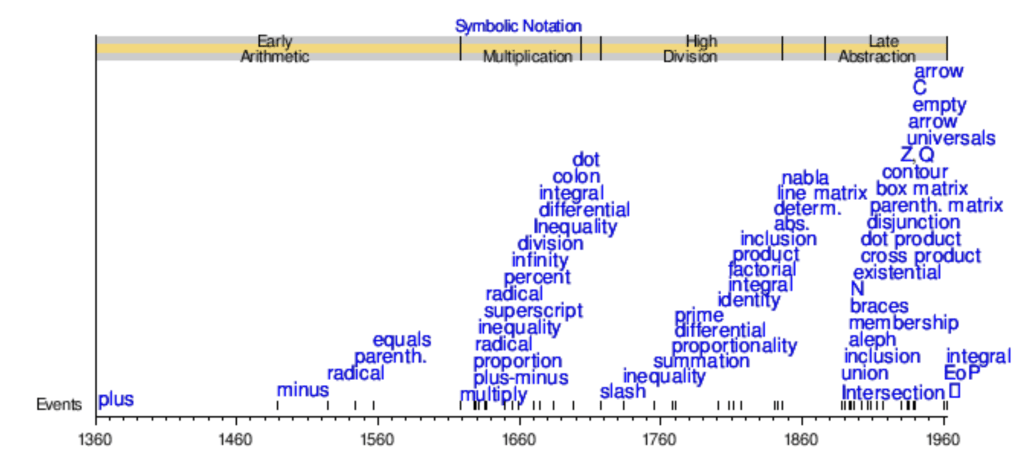
Before entering into the infamous metric system, let us dive deeper into the basics: mutual understanding. We have been dismantling what makes the “Western dominion” narrative so appealing; therefore, we need to look deeper at the foundational building blocks of our new age —where “humanity” can ask itself deeper questions. We have seen how commerce pushes connectivity and enables some basic communication, and how global standards emerge with the examples of timekeeping and mathematical notation. These, however, feel hopelessly limited for any meaningful exchange, as analytic philosophers discovered in the 20th century.

As with our thought experiment on first encounters, to establish an exchange one needs a basic set of communication rules. We have seen that pointing and smiling are human universals. These small gestures, in our thought experiment, allowed the initial connectivity of diverse groups of humans and contain the basic building blocks needed to create connections. To build upon that and ask complex collective questions, we need more sophisticated communication strategies. Fortunately, as illustrated, humans are born with such a strategy —or the capacity for it: language.

Indeed, if one looks at the history of many well-established exchange networks between different peoples, these are often associated with the development of a mutually understandable, but initially basic, pidgin language. As outlined, human brains seem to be made for this relatively easy acquisition of a second, third, fourth, or fifth language. Therefore, we possess not only the drive to learn a language but also the capacity to acquire additional ones —probably linked to the early onset of exchange networks in anatomically modern humans.

In the case of pidgins, these are even more interesting, as a common set of communication bits and pieces is put together on the fly by a diverse group of people who do not share a common language. Pidgins are a more or less complex set of communication strategies based on the languages already spoken by the peoples who come into contact, mixing concepts from different backgrounds. They first establish a basic shared vocabulary around a limited set of objects and actions, as is the case with linguas francas for trade and exchange. How easily pidgins can be constructed, and how organically they are established, further indicates that our brain seems to be built for social communication and for creating shared standards relatively easily, transmitting increasingly complex and abstract concepts that a language captures.

Depending on the depth of contact between the peoples with different backgrounds, the basic code —initially based on a limited shared vocabulary— can evolve to borrow the grammar of one or more of the languages involved. Grammar then becomes the scaffolding on which the vocabulary is built. These are the basic ingredients of a pidgin language. Pidgin languages then become more or less complex depending on the depth of contact, interaction, and areas of life that must be discussed. The most basic form is, as described, pointing, smiling, and saying a few shared words. At the other extreme is the creation of a brand-new language to be used by the descendants of the peoples in contact. At first, nobody speaks a pidgin as their first language. However, many of the pidgins associated with strong exchange networks have grown in complexity until they adopted all the characteristics of a fully-fledged language —spoken by many as a second language and eventually as a first language. At this point, this new language is often called a “creole”.

When a simplified language of a place is used as a trading language —while borrowing many, many, many elements from other languages— this creation is often called a lingua franca. The distinctions between lingua franca, “pidgin”, and “creole” are not clear-cut, and depend on how much influence one specific language had in the creation of the exchange code. However, in all cases, a lingua franca is not an exact copy of the parent language; it often includes vocabulary borrowed from other varieties and languages and always adopts a simplified grammatical structure.

In the case of Lingua Franca itself (or “language of the Franks”), it was in fact a commercial language spoken mostly in the eastern Mediterranean and North Africa. It was brought to these regions by North Italian (Genoese, Venetian, Pisan…) and Catalan sailors. It was not called Franca because it was spoken by the Franks or French, but because during the late Byzantine Empire, “Franks” was a blanket term applied to all Western Europeans due to their prestige after Charlemagne. In fact, over time, that language —used for commerce across the ports of the Mediterranean— was largely influenced by Italian dialects, Catalan, and Occitan more than by French. That early commercial language, lasting from the 10th to the 19th century, is what gave the name to the concept of linguas francas, or a functional language providing basic understanding between many trading peoples with different socio-cultural backgrounds. In this text, franca for short is a functional term, independent of any linguistic history or language structure. That concept can also be applied to pidgins and creoles, or whole languages like Hiri Motu —which is neither creole nor pidgin, but simply a franca from southeast Papua of Austronesian origins used for trading voyages.

Returning to the impressive Malay seafarers and traders, the current Malay language, or Bahasa Indonesia, is a language that originates from Old Malay, mostly spoken in Malacca —the great trading centre that the Portuguese conquered in 1511 CE. Old Malay, also known as Bazaar Malay, Market Malay, or Low Malay, was a trading language used in bazaars and markets, as the name implies. It is considered a pidgin, influenced by contact among Malay, Chinese, Portuguese, and Dutch traders. Old Malay underwent the general simplification typical of pidgins, to the point that the grammar became extremely simple, with no verbal forms for past or future, easy vowel-based pronunciation, and a written code that reflects the spoken language.

Back in 2016, I travelled for a few months through the Malay Peninsula and the Indonesian archipelago. During these trips I could easily pick up a few hundred words which allowed me to have simple context-based conversations despite my general ineptitude with languages. I was surprised by how much understanding could be achieved without even using verbs! The language had evolved such that verbs like ‘go’ and ‘come’ became prepositions like ‘towards’ and ‘from’, allowing me to build simple sentences describing my itineraries without proper verbs. This anecdotal example illustrates how Malay evolved to enable extremely easy preliminary communication.

But Malay is not only a franca. This is exemplified by the extreme complexity and nuance in vocabulary and verbal sophistication required to address your interlocutor based on their relation to you. You need a special way of addressing someone depending on whether they are a man, woman, young, old, or of higher, equal, or lower social status. This likely reflects the language’s other origin: High Malay or Court Malay, used by cultural elites and in courts, where making explicit hierarchical relations was (and still is) crucial.

Today, the language dominates the Indonesian archipelago, the Malay Peninsula and Brunei, and is also widely spoken in Timor-Leste and Singapore. In Singapore, however, the official and de facto trading language is English —but we’ll talk about that trading hub and English later. Malay is spoken as a first language by millions of people, but it is far more common as a secondary language, with almost 300 million speakers. Most of these speakers also know at least one other local language, like Javanese — spoken by nearly 100 million people— or Bazaar Makassar, another franca used by the Bugis, who historically landed on the shores of Western Australia for centuries.

Interestingly enough, modern Malay descends from a language spoken in ancient times in east Borneo. This language also gave rise to Malagasy, spoken by most of the population of distant Madagascar. The language arrived there via Malay seafarers and later traders. Afterwards, Bantu peoples from southeast Africa arrived and mixed with the Austronesians, giving rise to modern Malagasy —the only native language on the island (though it has three main dialect families). Apparently, nobody had the need to create new languages in this 1,500 km-long island.

The Bantu peoples themselves are also the carriers of one of the World’s largest francas: Swahili. It is spoken by up to 150 million people. Originating as a coastal trading language, it spread to the interior of East Africa, connecting the coast to the Great Lakes, and became a franca across the region and a mother tongue for many urban dwellers. It arose in present-day Tanzania during trade between the island of Zanzibar, inland Bantu groups, and Arabs (particularly from Oman). The Omani Imamate and Muscat Sultanate controlled Zanzibar and the Tanzanian coast during the 18th and 19th centuries and held considerable influence through the slave and ivory trade, among others. The name “Swahili” itself comes from the Arabic word for “coast”. Arabic has contributed about 20% of Swahili vocabulary, with words also borrowed from English, Persian, Hindustani, Portuguese, and Malay —the region’s main commerce languages. Like Malay, Swahili has a simplified grammar common in francas, making it easy to learn and pronounce. These traits have made Swahili a contender for a global communication language.

Beyond commercial francas, there are languages used exclusively as cross-border platforms for intergenerational communication, but which are not native to any sizable population. These languages are like frozen structures, called upon to allow a group of people to mutually understand one another.

Classical Latin is one early example of this function. By the 4th century, Romans were already speaking a language quite different from what Augustus spoke 300 years prior. Different parts of the empire used highly dissimilar versions of Latin, and Classical Latin served to maintain a unified system. That “old Latin” was standardised for literary production and, crucially, for imperial administration. After the division of the Roman Empire, the Western Christian Church also adopted a version of Classical Latin for internal operations: Ecclesiastical Latin. Previously, early Christians used mainly Greek and Aramaic —as we willl see.

Over time, Ecclesiastical Latin became the international language of diplomacy, scholastic exchange, and philosophy in Europe, lasting for around a millennium. It was not fully standardised until the 18th century! By then, linguists were eager to fix languages as words changed meaning too quickly —as the analyitical philosopher Russell observed. Ecclesiastical Latin flowed into the emerging sciences. The main works of Copernicus, Kepler, Galileo, and Newton were written in Latin.

But this Latin was a written language —no one really spoke it. And, unlike Swahili or Malay, it was far from easy to learn. Any Latin student knows how difficult it is to memorise its multiple, complex inflections. It became a written fossil spoken by basically no one —except a few geeks. That made the other nerd in the Peano-Russell nomenglature propose a simplified version of Latin, Latino sine flexione, as the  Interlingua de Academia. Peano, being Italian, had skin in the game. For us native latin languages speakers, such as my Catalan, a simplified academic Latin would be a great advantage compared to “ahem” we know what. But more on that and created languages to be international standards later.

Today, a stripped-down Latin does survive in science —particularly taxonomy, where the classification of living things (especially plants and animals) uses Latin binomials. For instance, humans are Homo sapiens, wolves are Canis lupus, and rice is Oryza sativa. Many scientific terms —especially in astronomy, physics, and cosmology— are still derived from Latin. So, through science’s dominance as the global system for classifying the world, Latin vocabulary lives on. It has become a kind of global pseudo-language, used by experts worldwide to communicate about shared topics but just as individual words, without any structural coherence.

Latin is but one example of an imperial language transformed into a franca and liturgical language. Another —and much older— example is Aramaic. Aramaic had the advantage of the simplicity of its written form. Unlike the complex cuneiform writing on clay tablets, Aramaic used a simple 22-character alphabet, which made it easier to learn and spread. This accessibility allowed it to be adopted in administration, commerce, and daily communication in a linguistically diverse region. The Achaemenid Empire adopted it as an administrative language, standardising “Imperial Aramaic” alongside Old Persian. Bureaucracy, scribal schools, and widespread official use helped it expand far beyond its original homeland —and its legacy lasted for over a millennium.

As with Latin, Aramaic became the medium of religious texts. Many Jews returning from exile after the fall of the First Temple continued speaking it. Scribes translated the Hebrew Bible into it, and large sections of sacred texts ended up in Aramaic. Other Levantine prophet religions like the Manichaeans also adopted it. One of these, Mandaeism, still survives, and its followers still speak a version of Aramaic. Eastern Christians adopted Syriac —an Aramaic dialect— for theology, hymns, and lengthy religious debates. Aramaic became the franca of the ancient Near East: everyone could participate. Thanks to that, like Latin, the language outlived the empires that spread it.

So, with these examples, we can begin to draw some principles for how linguas francas are established, spread, and sustained across space and time. They tend to offer accessibility benefits, borrow heavily from multiple languages, are often secondary but can become primary languages (especially in cities), and most importantly, serve specific purposes: commerce, administration, religion, or technical use. Perhaps we can even distinguish between written and spoken francas: spoken ones often have simplified grammar, are easier to pronounce, and accommodate mixed/macaroni forms. (Cool word, “macaronic” — look up its history!) Written francas, on the other hand, may retain complex grammar but offer easy ways to record text. Of course, ideographic systems like Mandarin or Japanese kanji present another accessibility puzzle —one we willl explore later, as they are closely tied to another leg of francas: formal state education.

In a world that is becoming more technical, more bureaucratic, and more formally educated, there is now ample space for new linguas francas to be established, maintained, and —for the first time— reach global scale. It is in these languages that we will begin to ask ¿what does humanity want?

Previous

Next