The sound of music

Posted on by wanderer

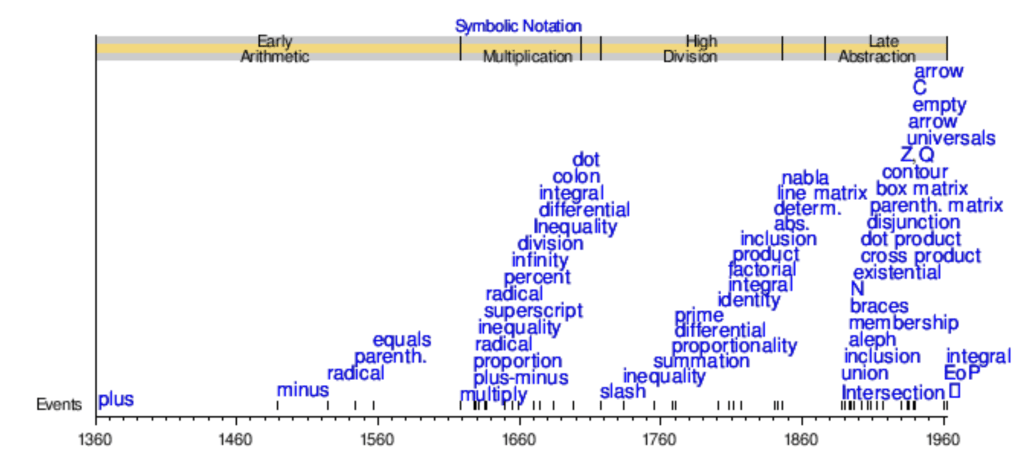
To keep postponing the Metric, let us explore another metric — the music metric. Since my music ignorance is as immense as music is —and i do deeply apologise to all he music lovers out there— I take metric to mean notation.

As we all know, sound is difficult to record compared to visual signals. Before the invention of gramophones and ceramic disks, the only way to play music created previously was either to have an unbroken sequence of people remembering how to play it, or to encode it in a system that could be reproduced later — either by other humans or by moving machines.

As always, the Greeks and Babylonians (Sumerians, to be exact) had already dealt with the encoding of music, but music is an immensely complicated language, and these scripts were only able to store the strings, the intervals, and tuning parts of the music.

The bit that is often told about the Greeks is the mythical Pythagoras. Beyond his triangles — which mostly were a well-established Egyptian knowledge — the Pythagoreans linked music and ‘harmony’ with mathematics, which they copied from the Babylonians this time. (Interestingly, the Chinese Shí-èr-lǜ scale follows the same logic.) Beyond copying and being attributed things he did not create, Pythagoras did make the musical and mathematical ‘divinity’ a religious sect by the 6th century BCE — if you want to perpetuate nerdy, complex, boring knowledge, you’d better make a religion out of it. In instruments, pitches, notes that were a half or 3/2 apart ‘sounded’ good. With strings, this is related to length, but also tension or tuning. Pythagoras and his followers could not resist giving this a ‘mystical’ meaning, trying to fit existence into his ‘divine’ vision — but reality, as it turned out, had other ideas.

What Pythagoras actually discovered — before wrapping it in mysticism — was that the harmonics of strings resonate with each other, a simple fact of physics that our ears have evolved to enjoy. From what we understand now, it is mostly a coupling of harmonics in strings and “overtones” in general. In other words, when an instrument produces a ‘pitch’, it gives off not just one pure wave but many smaller ones that resonate with it — and these combine to sound harmonious because they complement each other. Then, if you add another tone that also resonates with the primary frequency, or some of the overtones, that is also harmonious.

Our auditory system also resonates with nearby frequencies, which is why we find it oddly unsettling when two notes are almost — but not quite — the same. And there is a cultural layer on top. If you hear something that is slightly dissonant often enough, it will “sound good enough” not to care. It’s only when we hear music from another culture — one that divides its scales differently, using another temperament — that we start to notice those dissonances. Once your ear adjusts to the new metric, returning to the old one feels oddly off for a while.

And again, we go to Western Europe to observe the origins of most modern music notation. In this case, it started with the singing of prayers. As you can notice, voice is a continuum; there is no predefined ‘do’ or ‘re’. So voice, and music, had to be discretised into common units that everybody could ‘aspire’ to. This standardisation, inspired by the mathematical spirit of universality, was thought to be divine — which made following Pythagoras rather straightforward. Until it wasn’t (but more on that later).

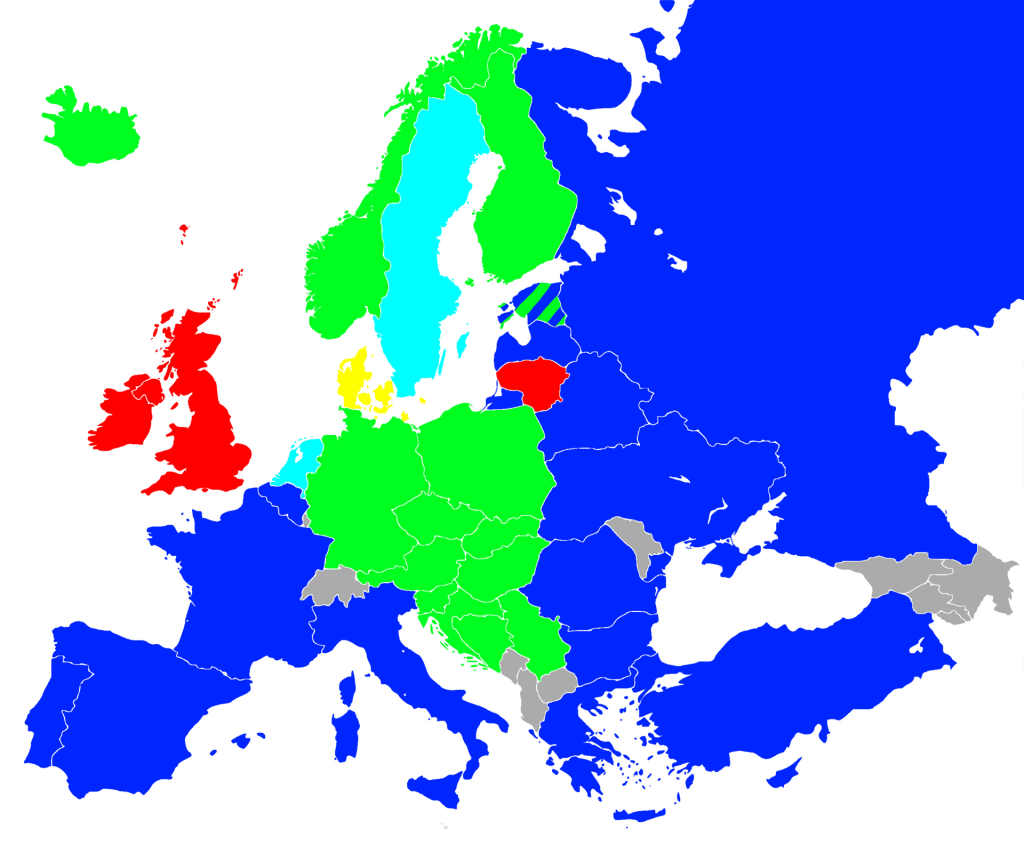
Before the well-known pitch system, what ecclesiastical choruses did by the 10th century was to annotate when the melody went ‘up’ or ‘down’ on top of the lyrics. Then a reference line was added to show the relative high and low of the melody. From there, by the 11th century, more lines were added above and below to structure the pitches in a standardised way. In parallel, it was necessary to know what the actual ‘pitch’ was, and that’s where the same guy who started adding the extra lines developed solmisation, with the familiar Do–Re–Mi–Fa–Sol–La–Ti (or Si) sequence appearing (though Ut instead of Do). This provided seven basic notes, which mirrored pre-existing scales like the Byzantine Pa–Vu–Ga–Di–Ke–Zo–Ni and the Indian svaras Sa–Re–Ga–Ma–Pa–Dha–Ni. This naming, however, was never fully standardised: the British preferred C–D–E–F–G–A–B (red in the map), as in guitar chords (E–A–D–G–B), while Germans and neighbouring regions (green, yellow, and sky blue) used C–D–E–F–G–A–H.

If one doubles around the central note, this provides the conventional twelve notes to be placed on top of the five-line staff developed by the 13th century. If you place a symbol on top of the five lines, plus four in between them, and two more on top and bottom, you have eleven spots; adding one more small line (a ledger line) at the bottom when needed is easy and gives the Babylonian twelve. At this point, we have something that looks a lot like the modern musical staff, or pentagram, and symbols that look a bit like the familiar ‘white’ [whole note], ‘black’, and ‘round’ musical notes. These symbols, known as ‘neumes’, took longer to standardise; there was still variety until around 1700, but by then most European notation had settled into the familiar form — even recognisable to a musically challenged person like me. Five thin lines, a ‘clef’ symbol at the beginning, and the pleasant ant-like procession of pitch along them. But like mathematics, musical notation is immense!

For the temperament, or tuning itself, Pythagorean (Babylonian and Chinese) fixing of the twelve notes to perfect ratios of 1/2, 3/2, 2/3 and their powers (C 1⁄1, D 9⁄8, E 81⁄64, F 4⁄3, G 3⁄2, A 27⁄16, B 243⁄128, C 2⁄1) failed because, contrary to belief, some of these pitches do not sound harmonious when played together — particularly something called the Wolf interval. It also made it difficult to shift the scale up or down beyond the twelve notes, since the spacing between them was uneven. To solve this, particularly for string instruments with many keys, like the piano, equal temperament became the standard by the 18th century, in which the distance between notes is, as the name suggests, equal. Developed independently in Europe and China in the 16th century, in mathematical terms each frequency interval is 1/12 of the octave (the distance between the highest pitch and the lowest), and the ratio between consecutive intervals is $^{12}\sqrt2$ — all equal in a logarithmic scale.

There is much more to it than that, and music notation and temperament have been evolving ever since, not unlike mathematics, with hundreds of signs emerging. Moreover, other familiar notations like the C–D–E–F–G–A–B guitar chords are ever-present. And music notation beyond the Western one is rich and diverse. But acknowledging my immense ignorance of music — and the fact that the basics have been quite established and spread around the world — I will limit myself to this standard that, like mathematical notation beyond numerals, has taken over the world.

From then — plus a few more inventions in tuning, non–string-pipe instruments, and electronic music among others — we have the fascinating fact that music written in one period can be played by future or distant musicians who have never heard it, as long as they possess the relevant knowledge and skill.

That transfer of sound into visual form (and back) is a truly fascinating invention — a collective effort across generations showing how sensory experience can be encoded, standardised, shared, and reinterpreted again and again. And, for better or worse, this very standardisation enables immense creativity while also stifling non-standard forms — a kind of ‘Western’ myopia, or more aptly, tone-deafness.

Thus, to recount: by the year 1800, and to this day, we have the following global or quasi-global standards — timekeeping, the calendar, mathematical notation, the Copernican principle, music notation, and temperament. These are not that many, but we will see that the other topics introduced — commerce and francas — will play a dominant role in the following two centuries.

Plus the infamous metric system! Nobody expects the metric system.

Prebious

Francas, Linguas Francas

Mathematics, universal not the way you think

Posted on by wanderer

Before moving to the quasi-universal metric system —which includes the archaic Babylonian timekeeping— let us focus on probably the first universal lingua franca: mathematics. And not mathematics as in “the language of the Universe”, but mathematics as in “the set of codes, rules, concepts, and ideas that are shared and approximately mutually understood by any human using them”.

As we will see, many linguas francas originate as an often simple code (compared to a general-use language), developed rather quickly to serve a specific function. In many cases, that function has been simple commerce and exchange, where the number of items to “exchange” is limited, and the rules of the game are simple —possibly including locally standardised accounting, such as produce and monetary units, and standardised measures like weights, surfaces, and volumes.

The linguistic and symbolic part of mathematics, therefore, is not so different from commercial linguas francas. What sets it apart is that, as of the 21st century, virtually everybody using “mathematics” as a functional system —mostly algebra and calculus— uses the same notation. In other words, it is universal.

This is not surprising: when one thinks about a universal language, one often refers to mathematics. However, like with timekeeping, how we came to the specific and well-known set of symbols +, =, ÷, ∞, … has its own history.

Mathematics and mathematical notation, although common in the current world, took centuries to take shape. Over generations, it was agreed upon by scientific, technical, and mathematical communities in Europe, the Middle East, and South Asia to use the same kinds of symbols, numbers, and conventions to refer to the same concepts.

Interestingly, these “concepts” themselves were (and are) thought to be universal, even beyond the human realm —i.e. the number 3 is the same in all parts of the Universe. Therefore, unlike goods and commercial language, which had local characteristics, mathematical notation is expected to be written in the same way by everyone using those concepts and wanting to share them, regardless of location. The same applies to signs and symbols like +, =, ÷, ∞, which any reader would most likely recognise regardless of the language being used.

For some reason, written mathematics —often calculus— has always been something of a special case in many cultures. We can write numbers as they are spoken in a given language —like zero, one, two, three in English, or cero, un, dos, tres in Catalan. But often, across many writing systems, numbers have been chosen to be represented by symbols, for example: I, II, III… (Roman, no zero), 0, 1, 2, 3… (Arabic, from South Asia), 𝋠, ·, ··, ··· (Mayan, perhaps the 0 doesn’t display in Unicode), 零, 一, 二, 三 (Chinese, 零 meaning something less than one, yet not nil).

These examples show that from early on, people decided it was better to simplify numerical notation —to the point that doing otherwise seems like suffering. Try writing down the year the Portuguese took control of Malacca in the Common Era calendar: one thousand five hundred and eleven, or one-five-one-one, if simpler. Write it. Stop reading.

How do you feel?

I bet it’s a pain, and it feels right to simply write 1511. A similar thing applies to phone numbers. If you’ve ever used certain online platforms that do not allow phone numbers to be exchanged, you cannot send them using digits. A workaround is to write them out in words —for example, “one hundred and twelve” or “eleven two” instead of 112. It’s not much more effort to spell the numbers, but it still feels like a pain knowing that a shorter, cleaner alternative exists.

Although people must learn two different systems to write numbers —instead of just the phonetic one— which might seem like more effort, in the long run, simplification tends to dominate. This preference for simplicity is similar to what we will see in francas, linguas francas: the adoption of a shared, simplified, functional language is preferred over a fully developed one. So, the basis of our mathematical universality might have less to do with the Universe and more to do with a universal feeling: tediousness.

In the case of mathematics, despite numerals having been used symbolically for millennia, the simplification of other concepts —like “sum”— into symbolic script is a relatively recent development. This is exemplified by the fact that signs equivalent to + are not found in many older written systems while there is a diverse set of equivalent signs to 1. Things like +, and -, are known as “operators” in mathematical terminology. Interestingly, many of these operation symbols —unlike some numerals that are simply dots or lines —have phonetic origins. Phonetic symbols were already present in some numerical systems, like one of the two Greek numerical systems, where they would use Π as five (short for pente, 5 —Π being pi, capital P in Greek), or Δ as ten (short for deka, 10 —Δ being delta, capital D). The other Greek numerical system simply assigned the order of the alphabet to the numbers, \alpha being 1, \beta being 2, etc. Many societies around the globe have developed advanced mathematical notations. However, none of them used algebraic notation like + to mean “sum”. Other mathematical systems worked with geometry to describe concepts, or used written linguistic statements.

Linguistic statements was the European method too. Before symbolic expressions, European mathematicians wrote their sums. For example, they would put on paper: “3 plus 5 equals 8”. Since that was a pain —like writing numbers in words— they simplified it to “3 p 5 e 8”. The operations had no proper symbols, just words or shortened initials understood by context. In fact, the sum symbol, +, is one of the earliest to appear in written arithmetic. Although it originated by mid-14th century, it was only commonly used by the 15th century. While there’s no universal agreement on its origin, it most likely comes from a simplified script of et, Latin for “and”, but nobody really knows why.

Algebraic notation to define operations was strongly promoted by the Andalusi mathematician Alī al-Qalaṣādī in the 14th century, where each sign was represented by a letter of the Arabic alphabet —for example, ﻝ for ya‘dilu (meaning “equals”). But it was actually a Welsh mathematician, Robert Recorde, who coined the modern equals sign (=) in the late-16th century. By that time, Europeans were mapping coastlines beyond Europe and the Mediterranean, Copernicus was posthumously publishing his Revolutionibus and the printing press was spreading like powder all over Europe —and people were still tediously writing “is equal to” or aequale est in Latin instead of just “=”. Try to make our kids do mathematics that way and see how long they can hold!

To be fair, most of the notation was standardised by the 20th century in the context of mathematical fields like set theory, groups, graphs, and others that most readers would not be familiar with. In fact, the evolution of mathematical notation and the stages at which one learns it in the educational system are uncannily correlated.

By primary school, around the planet, one learns the first symbols standarised by the 16th century +, −, =, ×, ., √ , ( ).

By mid-high school, one would learn the rest that can be easily written on a modern keyboard or a calculator with one or two keystrokes: ·, ⁄, %, <, >, ∞, ≠, xy , º, cos, sin, tan. These were developed by mid 17th century.

Once one goes on to study sciences in upper high school, one comes into contact with integrals, differentials, functional analysis, binomials: \int, \partial, x', f(x), \sum, \binom{N}{k} = \dfrac{N!}{k!(N-k)!}. These examples have linguistic roots too, but also “famous personalities” for example Newton’s binomial —Newton was known to have anger issues, that might explain the exclamation mark (!), though it was developed by Christian Kramp. More seriously, Newton’s arch-rival of all times, Leibniz thought that having the right notation was the solution to all human problems —if humans could create a universal logical language, then everyone would be able to understand each other. In the case of mathematics, Leibniz actively corresponded with his peers at the time to convince them that notation should be minimal. That, in fact, has informed most of our modern mathematical symbolism. Going back to our tedious exercise, this decision on minimalism might have a cognitive reasons, human operating memory is limited to about 3 to 5 items, and this storage lasts only few seconds, so it makes sense to develop notation that allows computation and arithmetic to fit well in that memory space. These symbols were common use by the early-19th century, though some, like \int, \partial by Leipzig were developed earlier or at the same time as the signs ·, ⁄ —these two being simplifications of the product and the division. Many of these symbols cannot be easily typed from your keyboard and need special code to type or display.

By the end of a technical degree like engineering or physics, one gets to know most of the mathematical notation developed by the mid-20th century, with scary things like tensors written using something called Einstein Notation: \Gamma^{i,j}_{k} —Einstein was known to be bored easily, that might explain that he preferred the simplified notation to the degree that dyslexic minds like mine mix these little indices.

Beyond these, one enters into advanced or specialised studies to learn the fancy ones: \rightarrow, \Cup, \exists, \forall, \vdash, \because, \therefore. Many of these are just substitutions of words that are mathematically “conceptualised”, like the numbers. For example, the Braille-looking \because, \therefore are just symbolic representations of the verbal statements “because” and “therefore”, respectively. Many of these symbols were developed during the late 19th to late 20th century. The most avid use of signs is in the field of mathematical logic, where Peano–Russell notation informs some its rules —Russell was a known geek, self declared to know nothing about aesthetics, that might explain his dislike of using words, which have the tendency to change meaning. Funny how he did not write much about the mostly aesthetical music, which has also a standarised quasi-universal notation, as we will see.

In short, in standard regulated education, one progresses through about 100 years of mathematical notation history every two or three years of modern study —although that is a non-linear accumulation. As one enters logic and set theory, the number of symbols needed run into the low hundreds.

Symbols by approximate “popular” introduction date

Nevertheless, the point at hand with mathematical operational notation is that it took hundreds of years to adopt the standardised form that is now widely used in all the teaching systems around the world. That evolution and standardisation did not happen in isolation, but were interwoven with other branches of knowledge, mainly technical ones. These technical fields needed the rapid adoption of simplified standards that could be learned efficiently by a specialised community of experts. This process can be understood, in part, in a similar way to how linguas francas are constructed —from a simplification of an already existing language— to be the means of exchange and understanding among a subset of people from many different cultural backgrounds who share similar conceptual and material items.

This notation is nothing new by itself. It is just a reflection of human needs —mutual semantic undertanding around a limited subset of concepts— and practical solutions that might have some cognitive biases. What is new is the fact that this notation reached a planetary scale. As we have seen with the spread of communication, that process is just a matter of scale, not of quality. But, in my view, that global scale makes all the significance and sets the question of this book. Mathematical notation, and its quasi-universal use, shows one paradigmatic example of how we arrived there. How we arrive there, or not, and a standard is kept regional, is significant.

Mathematical notation has been the first of such lingua francas to become a standardised language used across the whole planet. It is, however, limited to be used only by someone who needs to do arithmetic —which, in our case, is anyone who has entered a regulated educational system. As we will see, regulated educational systems have reached over 80% of the human population, and are implanted in virtually every new human being born.

Now we have the example of how a truly global language —albeit a limited and specialised one that rides on the back of the universality of what it studies— is created, adopted, and made universal. In particular, this one has been made universal without any clear agreement or premeditated guidance, but rather by the sheer pressure of technical needs and the dominance of Western knowledge systems. Same as with time keeping. Time-keeping, by the way, will come back, and we will see that the universality actually is held by technical needs, mostly as a matter of sailing ships, driving trains and flying planes around the world while knowing where you are also in space.

So, the World has not finished with mathematics as universal communication, other technical and symbolic language are coming. The Metric System is coming, and this time, with bureaus.

Previous

Time keeping

Next

Francas, Linguas Francas

Revolutions, Scientific Revolutions

Posted on by wanderer

The peoples that embarked and supported the exploration of new trading and colonising routes soon discovered that the free-riding of the technological advantage could be easily perpetuated. Thanks to that, the ones that invested in better and faster understanding of the world, plus the technical innovations that that understanding and implementation represented, contributed to a further control of the world’s connectivity. From that on, there were no major barriers to a hyperconnected world. What they could not control by exchange, they would control by overpowering, as the conquest of Malacca, the Aztecs, the Incas demonstrates. If you kept on expanding your technological and resource allocation dominance over other peoples, your system would be the one to dominate, and that’s exactly what the Western nations did over a period of a few centuries.

New trading routes led to an excess of wealth that could be poured into more navigational sophistication, which in turn would make the trading networks more reliable and affordable, freeing more resources for further improvement. Part of these resources went to the birth of modern science, changing forever the way our understanding of the world was established.

To make a boat sail safely from port to port you would rely less and less on divinity and more on your instruments, navigational skills, the capacity to understand the sky, star positions, read the winds, proper sails, masts, ropes to withstand storms, carrying lemons to stop scurvy, social structures to govern a ship and stop mutinies, etc. Those powers that would put scientific knowledge to good use would have in their hands better control of the high seas and the peoples cruising them. Likewise, those who understood better the fabrication techniques could build better vessels, and equip them with better weapons. On the other hand, the faraway encounters would contribute to the scientific understanding of the world, like sea currents, Volta do mar, steady trade winds, or even catamaran technology from the Pacific and front crawl swimming techniques from North, South America, or South Africa.

In fact, Columbus’s error regarding the radius of the Earth (which he was convinced until he died) was due to the preliminary stages of scientific knowledge attempting to describe the world we lived in. In that case, he was mistaken, but the geographers’ community soon recognised the error and corrected it (or lent more credibility to other estimates circulating at the time). This iterative process helped to better understand the world that was opening up before them as they tried to cartograph the new routes faster than they were explored.

From these explorations and shocks to the perceived worldview, it is not difficult to imagine that the notion of an entire landmass the size of the Americas suddenly appearing on maps (over about 20 years) might have led to the acceptance of rethinking the entire Universe. If the Earth contained a whole part of itself that was unknown to the Old Scriptures, how much more knowledge might be out there—waiting to be found, explored, and understood—not through the lens of the Scriptures, but through the lens of something new? These cartographic shifts might easily have been the seeds for scientific enquiry—the seed of the Scientific Revolution.

In fact, it is interesting to reflect on that word, “revolution.” What does it stand for? It comes from the root “to revolve”, which means to spin around. Why—if an entire continent had been missed, and Jerusalem is not the centre of the Earth—could it not be that the Earth is not the centre of the Universe either? That kind of thought might have helped Copernicus push the heliocentric idea: that the model best suited to describe the Universe is not a geocentric one, with the Earth at the centre, but one with the Sun at the centre of the known cosmos. Copernicus was not the first to propose that idea; the Pythagoreans had already supposed the Earth might move, and Aristarchus of Samos proposed a heliocentric model in the 3rd century BCE. Seleucus of Seleucia said something along the same lines in the 2nd century BCE. About 600 years later, in the 5th century, Martianus Capella, from Roman Carthage, proposed that Mercury and Venus spun around the Sun. At about the same time, Aryabhata in Patna, India, proposed that the Earth spins and that the planets orbit the Sun. In the 12th century, Ibn Rushd (Averroes) and Nur ad-Din al-Bitruji of the Cordoba Caliphate were also critical of the geocentric model and proposed alternatives. Their views spread into European intellectual spheres. However, none of these theories gained much traction at the time they were proposed. One can say that the mindset of the people of those generations was not particularly open to such a shift in worldview, nor was it needed for any practical purpose.

To be open to other worldviews becomes more likely if a sweeping 30% extra landmass is literally put on the map. The same world that the Scriptures plus Classical Philosophy were so certain they understood. Even though the Catholic Church did not pay much attention to the fact that the world was different than said, surely minds would become more open—even if obtuse. Moreover, those same conceptualisations ended up making navigation more precise. And the required navigational observations and technical means (star and planet positions, astrolabes, compasses, telescopes, clocks…) helped to question the worldview in a more rigorous way—with the newly discovered facts holding more face value than old beliefs. In short, cosmological views came to serve a practical purpose.

Therefore, the landscape was set. After Europeans became aware of a New Continent, Copernicus was able to push his idea (initially as a short leaflet in 1514), and later publish, after his death, his De revolutionibus orbium coelestium. His heliocentric model was not the one we know today. Copernicus’s model was not that innovative, nor significantly simpler than the Ptolemaic one, because he still needed the use of epicycles (small circumferences around the circular orbit of the planets) to accurately describe the rotation of the planets around the Sun. It would be Kepler—about 70 years later—who, after throwing out his own Mysterium theory of planetary movement because Tycho Brahe’s observations did not match, solved the motion of objects in the Solar System with simple elliptical orbits and delivered us pretty much the view that we now have.

Even after the heliocentric vision of the World was presented, the conviction of perfectly circular orbits was not abandoned, here a drawing trying to explain the elliptic orbit of the moon (Luna) around the Earth (T) with three epicycles. Calculations according to Schöner’s Tabulae resolutae and Reinhold’s Prutenicae Tabulae in lecture notes from 1569

The difference with all the previous scholars—after Copernicus’s posthumous publication—proposing that the Earth was not static, was that the public at the time was much more accepting of the revolution of the Earth thought. A thought that would be revolutionary!

Revolution, at the time, had the meaning that Copernicus used in his title: simply the spinning around of the celestial bodies—how they revolved around the Sun. Revolved, revoluted, revolution. It was a physical description, like that of the revolutions or cycles of an engine, or as one famous revolutions podcaster puts it, “coming full circle”, just to come back to the beginning. Revolution did have, on rare occasions, the meaning of change prior to Copernicus’s work. However, the acceptance of heliocentric theory by the public of the time. It was so disruptive to the mindset of the age, overturning millennia of knowledge and worldview—so Earth-shattering (pun intended)—that the first main word of the work itself, revolutionibus, was adapted less than a century later to mean the overthrow of a political system (the Glorious Revolution in Britain). When transferring the physical meaning to the political one, revolution meant “a circular process under which an old system of values is restored to its original position, with England’s supposed ‘ancient constitution’ being reasserted, rather than formed anew”. At that point the use of the word was far form the meaning that it has now, as a radical new direction, or changing of course of what was before. Soon after, however, the word gained the modern concept of revolution, as used for the French one, which probably someone has heard about. Now revolution is more widely understood as the shattering of a previous political, social, technological—or otherwise—system, and the establishment of a new one: the Glorious Revolution, French Revolution, Industrial Revolution, Agrarian Revolution, Sexual Revolution…

It could be that the people at the time—after the Earth had been kicked aside, given rotation, put in orbit around the Sun, and the stars made still—experienced a mental shift so profound that it allowed for a reshuffling of many pre-existing mentalities. Maybe it can be compared to the shattering effect, almost a rite of passage, that many children in the Western world experience when they realise that Santa Claus is not a real being, but a construct created by society to make them believe that the bringer of presents is this exotic figure from faraway lands, and not their parents or families. For the child, it is already a big impact—and if you experienced that, you probably remember the moment, even if it was decades ago. Then imagine if instead of just one child at a time, it were an entire society realising, more or less simultaneously (within a generation), that the reality they had so strongly believed to be true, no longer was. That is what the so-called Copernican Revolution brought to European thought in the 16th century: a collective, mind-shattering effect. We, as humans, have been toying with these moments ever since. But more about that later.

In fact, the public that was more open to these ideas was also in the midst of another revolutionary movement, which at the time was called a protest, for lack of a better word: Protestantism. If the world, the solar system, the Universe, the Cosmos, was not as the Church claimed—with extra continents unaccounted for, the Earth in motion, and stars being other suns, perhaps with other Earths—then the Church became open to protest and reform. And if protest and reform were possible, then the acceptance of truly exotic ideas—like the Earth revolving—became easier in a society already undergoing profound transitions. In fact, different solar system models were readily adopted by Tycho Brahe and Johannes Kepler, Danish and German astronomers sponsored by Protestant-friendly kings. Meanwhile, Latin astronomers such as Galileo Galilei and Giordano Bruno had major conflicts with the Catholic Church in Northern Italy—Galileo famously tried, Bruno burned at the stake. Bruno’s seven-year trial and sentence to be burned alive was not specifically for his belief that the stars in the sky were other distant suns orbited by other planets, but also because of his rejection of most Catholic doctrines.

The difference between Copernicus in the 16th century and all those who proposed alternative cosmological systems before might be that society was more open to new ideas because of empirical slaps in the face—steadily, repeatedly, forcefully. First, sailors and their investors realised that direct observations could actually shift reality—such as the discovery of a continent, accurate measurement of latitudes and longitudes, and the real size of the Earth’s circumference. Second, astronomers and their sponsors (who were often astrologers for European courts—better predictions meant better horoscopes; the zodiac pays for your smartphone, if you think about it) found that when your health or the outcome of a war depends on the conjunction of Saturn and Jupiter, and your astronomer looks through a telescope and tells you that these planets have rings and moons orbiting them, you might predict better when to wage your next war. Third, traders could more precisely calculate profits or invest in new products—like new dyes and pigments (e.g. scarlet), or learning how to plant species such as pepper, potatoes, tomatoes, tobacco, coconuts, sugar cane, among others, across the world. Actual measurements began to overturn established doctrines one after another; these facts reinforced the critiques of the old system and laid the foundation for an alternative system of establishing knowledge. The Scientific Revolution went hand in hand with the development of better instruments and measurements that define the modern world we experience today.

It was equally important that these new ideas travelled and multiplied faster than ever before. On one hand, naval interconnectivity regularly reached all continents and the major inhabited landmasses of the planet. From there, peoples—willingly or unwillingly—became part of a shared system of exchange, a process that continues today, where nearly every human being is regularly connected to the rest of the world in one form or another. Our present hyperconnected world is extending the reach and frequency of connection to ever more remote places. On the other hand, the printing press allowed for the multiplication of ideas at a rate faster than authorities could suppress them. Even if the works of figures like Copernicus or Bruno were censored, confiscated, destroyed, or burned, it was much more likely that one copy would escape, be read, and be copied again. Before the printing press, Protestant ideas—like those of the Hussites in the 15th century—did not spread far beyond their place of origin (e.g. Bohemia). Later, Prague—with its famous astronomical clock—would host Brahe and Kepler. On the other end of the chain, at the point of reception, Spanish missionaries actively protected indigenous languages (while simultaneously suppressing their cultures) in regions such as Mesoamerica, the Andes, and the Philippines, to prevent indigenous peoples from being exposed to “dangerous” Protestant, Enlightenment, or revolutionary ideas. To this day, these regions preserve some of their linguistic diversity and remain heavily Catholic, with the Philippines being the only nation (alongside the Vatican) that does not permit divorce.

Our hyperconnected and idea-copying world is the one that gave birth to the concept of humanity—a “humanity” that can now begin to ask itself what it wants to do, now that we have the means to communicate with one another, and the resources (or energy levels) to invest a fraction of that energy in specific goals. But before asking that question, we first need to understand the mechanisms by which a hyperconnected people is able to pose it: which networks are activated, in which language communication occurs, with whom that exchange is implemented, and what actions can—or cannot—be taken. What is the agency?

Curiously, one of the early adopters of Copernicus’s thesis was Thomas Digges, who removed the need for the sphere of fixed stars. He proposed the existence of distant stars scattered throughout the Universe. This led him to raise the paradox of the dark sky: in an infinite Universe filled with stars, the sky should look like the surface of the Sun, because in every direction there should be at least one star. Since the sky is black, the Universe cannot be infinite. With that in mind, the Copernican Revolution—which displaced us from the centre of the Universe—is still not complete. It is geographical, but not temporal. Heliocentrism kicked the Earth and its peoples out of the centre of space, but the dark sky placed us in a special time—a time when we can still see the horizon of the visible Universe. Now we are in another special time—the time when humanity is conceptualised. The time to ask: what does humanity want?

Previous

From the neighbours to the oceans

Next

Western dominions

Growth of communication- Culture

Posted on by wanderer

All of the previous examples I have highlighted until now, show living beings collaborating and cooperating require a basic feature: communication. Communication involves shared channels in which the individuals that form a group or interaction have cues and signals that can be understood by other members and entities. These are mainly visual, chemical, acoustical, and vibrational cues. With these cues, the basic structure of formations larger than the individual exists, allowing for the generation of other ways of interacting with the environment that individuals alone cannot achieve.

Out of the three bases of global reach (intelligence, collaboration, and communication), I will focus on communication as the most critical for our understanding of how we got here—that is, the capacity to communicate at many and diverse levels and across a wide range of scales. From really superficial to deeply technical ones, from proximity to global.

At some point in this arrangement, a complex cognitive structure emerged in the form of language. This sophisticated communication would encompass most forms of categorising the external and internal world of individuals in any group united by communication. Many debates concerning the limits of knowledge originate from analysing where our knowledge of the world around us is constrained by language. These debates span back centuries, for example G. Berkeley’s, A Treatise on Principles of Human Knowledge (1710) or J. Locke’s Essay Concerning Human Understanding (1690), or take really interesting forms, like the Sapir-Whorf effect, where language might shape the essence of how we see our world. For example, many languages do not have words for numbers larger than 3 or 4, but might have hundreds of words for different scents, which we lack.

In any case, at some point language was used not only for the communication between members of in-groups, but also with external groups, becoming a federation of groups, as anthropological research shows. That is where everything really changed, where “Culture” emerged in the sophisticated form that we know and where information, collaboration, exchange, reduction of conflict and complex networks would extend the wealth of possibilities of how interact and shape our environment. This level of inter-group communication is something that has not been achieved successfully by any other living thing on this planet —maybe with the exception of the Fire Ants, and they are a only doing it for the last 100 years or so. As humans, we achieved the creation of a structure —culture— which allows detailed communication between virtually all the members of our species.

Once communication between groups emerges, everything changes. This accumulative communication allows for the complexity of the tools we use to be open-ended, as the evolution of technology and tools like large particle accelerators or space satellite constellations shows.

Communication is also open-ended, meaning that it can potentially keep increasing indefinitely, probably linked to the complexity of tools. In nature, communication channels tend to be very limited and do not show growth or evolution by themselves, while human languages are always in continuous evolution—incorporating new concepts and terms, combining existing ones, losing or forgetting others, and actually forging what is needed. This applies not only to language but also to symbols, signs, experiences, training, repetitions, etc. This indefinite addition of communication elements adapts to achieve the desired level of communication, understanding, and sharing of the initial information. To put it simply, to pass on a specific message. This depth of communication also requires boundless collaboration to construct the complex concepts needed for sophisticated knowledge.

All in all, this open-ended way of sharing messages has created what we have come to know as culture and cultural evolution—the body of messaging and knowledge that is passed from one generation to another, with the capacity to add new pieces to that pool or lose them. Moreover, we have, in principle, the limitless capacity to transmit accumulated knowledge and messages to other human beings, as long as there is a shared communication channel.

Collaboration <- Previous Next -> Language

Preface

Posted on by wanderer

¿What does Humanity Want? seems like a simple, obvious question to ask. However, what is most striking is that we ask this question at all. The fact that we can even pose such a question reveals a complex set of circumstances that have emerged for the first time in human history. The question is a product of the unique times we live in—shaped by global interconnectedness, globalisation, conceptual homogenisation, and the dominance of a single philosophical and legalistic strain over the rest of the world. These circumstances establish a minimal set of elements that are either shared or imposed on virtually all creatures we call “humans.” By asking this question, we are exploring what defines us, what makes these times special, and what historical and temporal currents have allowed us to even contemplate what humanity wants.

If we break the question down, it revolves around two key terms: humanity and want. The concept of “humanity” is relatively recent, although it has deep historical roots. On one hand, the idea of what it means to be human is, while intuitive, not perfectly defined. In this text, we will examine how the concept of “humanity” came into being, what it represents, who created it, and what status “humanity” holds in the modern world. We will explore who is included within this term, who might not be, who defends it, who opposes it, who speaks “in the name of humanity,” and what that entails.

On the other hand, there is the term want. If defining “humanity” is challenging, “want” is infinitely more complex. Determining what the aggregation of these “humans” living on this planet (or orbiting it) “want” is nearly impossible. We will focus on who within humanity has the agency to “want” something, what is meant by “wanting,” how these wants are determined, and how resources are allocated—or not allocated—to fulfil them. By “want,” we refer to all actions related to a shared consciousness. These actions are taken by individuals, groups, or institutions who claim to represent humanity. We will explore what they “want” to do with this concept of humanity—or whether they can do anything at all. Along the way, we will discuss the limits and capacities of these groups to decide on humanity’s wants, the resources available to them, and the obstacles they face. Finally, we will consider a few possible paths forward, alongside the difficulties inherent in pursuing any of them—or none at all.

Before addressing the core question, this text will first tackle another fundamental one: Why? Why are we even able to ask this question at all? To answer this, we will embark on a journey through time and space. We will begin with humanity’s deep roots in biology and evolution, examining what we share—and do not share—with our fellow living beings. Our journey will navigate geography, science, philosophy, linguistics, academia, history, politics, economics, narratives, and fictions to situate us within this unique moment in time. The aim is to inspire both reflection and action. So, buckle up and enjoy the ride!

We live in extraordinary times. When viewed through the long lens of history, it becomes clear how exceptional this moment is. We are riding the upward curve of exponential growth in all attributes that define humanity. This growth brings with it unprecedented opportunities and challenges, forcing us to rethink how we honour the past, live in the present, and plan for the future. For the first time, these considerations can occur at the level of a collective imagination. Planetary-scale decision-making—a concept only recently conceivable, such as Psychohistory from Asimov—is now part of our reality.

This unique awareness allows us to ask the question central to this text, which compels us to consider what it means to exist in this state of affairs.

This is not an entirely new idea. In 1933, George Orwell observed in Down and Out in Paris and London that humanity was already living in a time where technological development could ensure that the global population was adequately fed, with resources to spare. For Orwell, the fact that this was not happening was a crime. While Orwell may not have explicitly framed his argument in terms of “humanity,” he recognised that resources were being misallocated due to misplaced priorities—especially by those who controlled production and logistics.

In the following essays, we will unwrap how we arrived at the point of asking this unique question: Who can ask it? How? Why? We will explore potential answers, possible solutions, and whether there are any viable alternatives to this trajectory of planetary, collective resource allocation.

Foreword <- Previous Next -> Opening

Disclaimer

Posted on by wanderer

In these texts, I attempt to answer the question: “What does humanity want?” I approach this from the perspective that, for the first time in human history, we have the means to ask ourselves this question and set aside a fraction of our resources to act upon an answer. However, I wish to emphasise that the ability to ask this question is neither inherently good nor bad—it simply is—and to be able to ask it represents a new phenomenon on our Planet.

I want to stress that asking it is not a sign of grandeur or having achieved something superior. It is not as though this represents a greater good we should aspire to, nor is it the only possible outcome for humanity, as if dictated by some kind of divine providence. There are countless other paths in which humans might never have arrived at this point. It is not a “manifest destiny”; it is simply the reality we find ourselves in at the moment.

For now I want to preemptively suspend moral judgement in order to assess the question itself and the possibilities it presents. From that moral suspension, we may be able to ask ourselves what we want to do, and with that awareness and consciousness, we can build upon this knowledge—both critically and appreciatively—of the state of the world in which we find ourselves.

That said, it is important to highlight that there are moral considerations attached to the decisions we make regarding what to do with the awareness of the question.

A significant part of the book is dedicated to analysing and investigating the routes that brought us to the point where we can ask this question. Some of these routes involve the destruction of many cultures; the extinction of global eco-cultural diversity; the growth of administrations and institutions that impose restrictive measures on their populations and others around the Globe; wars of conquest; the deaths, killings, and murders of millions of people, genocides; all the spectrum of suffering experienced by human beings, individually and collectively; the imposition of world-views in the ongoing ethnocide, the destruction of ways of life and world-views, languages, and traditions; the overwhelming dominance of a cultural might; abuse of power; the use of technology to subjugate other peoples, among others.

I want to make it unequivocally clear that I am not at all justifying or condoning these events, nor am I grateful for their occurrence because they allow us to ask the question posed in here. On the contrary, I strongly condemn the list above, and I would much prefer they had never happened. I would be happier if humanity did not possess these qualities and did not take these actions in the past. Nevertheless, we must acknowledge that these past acts are part of our path to the present, part of our ancestry and legacy, of our shadows. As the saying goes, those who fail to learn from history are condemned to repeat it. If the question behind these writings serves any purpose, it is to make us aware of that dark side and to help us decide whether it is acceptable in the present and in a possible future. I have stated my moral position here, but I recognise that it may not be shared by all.

On the other hand, if we indulge in “what if” scenarios of alternative histories, our World might look very different, and this question might not even arise. However, that is not the point. What matters is recognising that the items on the list of shadows are, by most accounts, considered terrible events, and yet they are also part of who we are and how we came to be. The lesson here is to learn how to act with this knowledge and awareness, much like young children learning to redirect and control their anger. We cannot deny our childhood and the ways it has shaped us, but we can learn to behave in a manner we consider appropriate for the times in which we live—with the extra resources, responsibilities, and nuances of adulthood.

Our current era presents a unique opportunity to explore the ways we can take action to avoid repeating the dark past—or, at the very least, to determine whether such an endeavour is possible or merely a pipe dream.

Overview <- Previous Next -> Foreword